【微分は接線の傾き】なぜなのか！？そのイメージをアニメーションで徹底理解！！

　ここでは微分が接線の傾きを表すイメージを得ることを目的にします。アニメーションを通して曲線も超拡大すれば直線なのだと納得し、limやdx,dyといった記号の意味・気持ちが分かります。

微分の定義とイメージ：超拡大すれば直線
微分の定義と導関数：結果は意外に簡単
まとめ

微分の定義とイメージ：超拡大すれば直線

定義式はとっつきにくいのでアニメーションでどうぞ

　例えば $f(x)=x^2$ を $x=1$ で微分することを例に考えます。微分の定義式により、

$$f^{\prime}(1) = \lim_{h\to 0}\frac{f(1+h)-f(1)}{h}\tag{1}\label{p7eq1}$$

ですが、この式変形がどうもとっつきにくい。また、この式を理解したところで後の問題にもあまり有効でない。そこで、ここではこの式の気持ち、イメージを理解することを目的にします。このアニメーション(以下、動画)です。

微分のイメージは超拡大すること

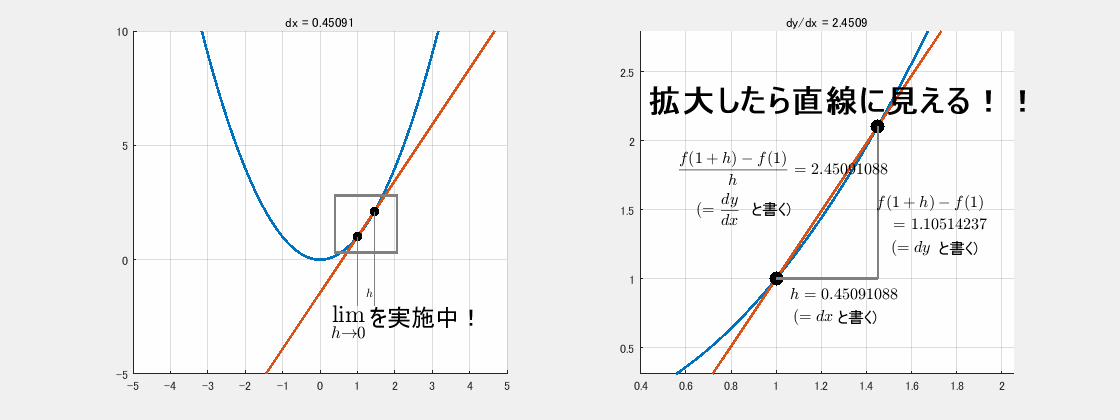
　アニメーションより、$y=f(x)=x^2$ の $x=1$ における微分 $f^{\prime}(1)$ とは、

$y=f(x)=x^2$ の $x=1$ 付近を超拡大●●●

したものであることが分かります。超拡大したら青の線と赤の線はほぼ重なりました。つまり、

曲線も●●●超拡大したら直線●●になる

ということです。

微分のイメージと $\lim_{h\to 0}$ との関係

　動画ではこのことを理解するために、あえて少し離れた $h$ から始めて拡大しています。動画の最初と最後のコマを静止画にしたものを下記に示します。

これは、動画の最初のコマです。

最初のコマでは傾きを調べる横幅 $h$ を $h=1$ にしています。そのときの傾きは $3$ です。左の図と右の図は同じグラフですが、描画範囲が異なることに注意してください。動画をスタートさせると $h$ がだんだんと小さくなってきており、それに対応して右側は拡大しています。動画ではその気持ちを左の図に「$\lim_{h\to 0}$ を実施中」と表現しています。

$\displaystyle\frac{dy}{dx}$ の気持ちは分数

　そしてこれは動画の最後のコマです。

最後のコマに近づくと途中からなぜか、「$dx$ と書く」とか「$dy$ と書く」とかが出てきています。横幅 $h$ が限りなくゼロに近づいたとき、横幅 $h$ はもはや $dx$ と書く気持ちになります。同様に、その時の縦幅($=f(1+h)-f(1)$)は $dy$ と書く気持ちになります。そうすると、微分記号である $\displaystyle\frac{dy}{dx}$ はあたかも分数のように感じ、まさに「傾き」を表している気持ちです。

まとめ　微分のイメージは超拡大　地球と私

　このように微分とは、左の図では「接線の傾き」であり、右の図では「超拡大したときの（元のグラフの）傾き」です。どちらも同じことで、巨視的に見れば左図で、微視的に見れば右図のようだということです。例えれば私たちが普段住んでいる地球です。地球規模からみれば微視的世界に住んでいる私たちは、自分の周りの世界が丸まっているなどとは感じず、平面であると感じます。微分とはそういう感じで

微視的世界で見たときにどう見えるか

を考えています。

微分の定義と導関数：結果は意外に簡単

微分の定義式から $y=f(x)=x^2$ の導関数を導く

　上の図で見たように $y=x^2$ を $x=1$ 付近で超拡大したら傾きが $2$ の直線に見えました。それを式変形で求めます。

\begin{eqnarray}
f^{\prime}(1) &=& \lim_{h\to 0}\frac{f(1+h)-f(1)}{h}\\
&=& \lim_{h\to 0}\frac{(1+h)^2-1^2}{h}\\
&=& \lim_{h\to 0}\frac{(1^2+2h+h^2)-1^2}{h}\\
&=& \lim_{h\to 0}\frac{2h+h^2}{h}\\
&=& \lim_{h\to 0}(2+h)\\
&=& 2
\end{eqnarray}

となり、求められます。余談ですが、動画の最初のコマでは $h=1$ でそのときの傾きは $3$ でした。これは最後から一つ前の式 $\displaystyle\lim_{h\to 0}(2+h)$ で $h=1$ を入れれば $3$ になることに対応します。

話を元に戻し、今はたまたま $x=1$ 付近を超拡大（微分）しましたが、$x$ をそのままに式変形をすれば、任意の場所で超拡大したときの傾き（微分係数）が得られます。つまり、式$\eqref{p7eq1}$の1の部分を $x$ に戻して計算を進めればよく、

\begin{eqnarray}
f^{\prime}(x) &=& \lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\\
&=& \lim_{h\to 0}\frac{(x+h)^2-x^2}{h}\\
&=& \lim_{h\to 0}\frac{(x^2+2xh+h^2)-x^2}{h}\\
&=& \lim_{h\to 0}\frac{2xh+h^2}{h}\\
&=& \lim_{h\to 0}(2x+h)\\
&=& 2x
\end{eqnarray}

となります。これが、$y=f(x)=x^2$ の導関数です。

$f(x)$ に対して $f^{\prime}(x)$ のことを導関数と言います。したがって、微分することを導関数を求めるとも言います。

$y=f(x)=x^n$ の導関数

　一般に、

$f(x)=x^n$ を微分すると、$f^{\prime}(x)=nx^{n-1}$

となります。これは覚えなくてはいけない式でうんざりしますが、そう考えるよりも、式$\eqref{p7eq1}$ のような面倒な計算をしなくても求められると考えれば少しは気が楽になるのではないでしょうか。

$\displaystyle\lim_{h\to 0}(x+h) = x$ の気持ちは「おおよそで考える」

　この式、$\displaystyle\lim_{h\to 0}(x+h)=x$ はもちろん、

$h$ を限りなくゼロに近づけるのだから、$x+h$ は限りなく $x$ に近づく

ということを表現しています。

ここではそのことをもう少し緩くとらえてみます。$h\to 0$は、$x$ に比べて十分に小さい、だから $h$ はゼロとして考える（「無視する」と表現することが多い）、ととらえます。これは言い換えれば、大体こんな感じだよね、ということで済ませている気持ちです。上で見た「曲線も超拡大したら直線」も結局は、「本当は曲線だけど、（これくらいの狭い範囲 $h$ では）おおよそ直線と考えていいよね」という気持ちです。

他よりも極端に小さいものは無視してしまって、おおよそで考えるという気持ち

まとめ

　動画を用いて微分のイメージを得ました。それにより、