24年度の入試問題です。難関大学の入試問題には本質的な学びにつながる良問が多いです。ここでは名古屋大学、慶応大学、京都大学(文系)の問題を取り上げました。問題の解説にはアニメーションを用い、イメージしやすく分かりやすくしています。
名古屋大学
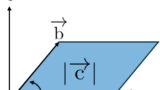
座標空間の3点 A(3,1,3), B(4,2,2), C(4,0,1) の定める平面を H とする。また、
→AP=s→AB+t→AC (s,t は非負の実数)
を満たすすべての点 P から成る領域を K とする。
(1) 内積 →AB⋅→AB, →AC⋅→AC, →AB⋅→AC を求めよ。
(2) 原点 O(0,0,0) から平面 H に下した垂線の足を Q とする。→AQ を →AB と →AC で表せ。
(3) 領域 K 上の点 P に対して、線分 QP 上の点で →AR=r→AC (r は非負の実数) を満たす点 R が存在することを示せ。
(4) 領域 K において原点 O からの距離が最小となる点 S の座標を求めよ。
平面のベクトル方程式です。一般事象はこの記事↓で詳しく解説しています。
領域 K は下記の薄い青で塗られている部分です。

→AB, →AC はすぐに使うのでここで求めておきます。
→AB=(422)−(313)=(11−1)
→AC=(401)−(313)=(1−1−2)
(1) 内積を求める
(1) 内積 →AB⋅→AB, →AC⋅→AC, →AB⋅→AC を求めよ。
解
→AB⋅→AB=(11−1)⋅(11−1)=3
→AC⋅→AC=(1−1−2)⋅(1−1−2)=6
→AB⋅→AC=(11−1)⋅(1−1−2)=2
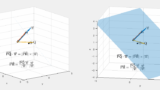
(2) 垂線の足 Q
(2) 原点 O(0,0,0) から平面 H に下した垂線の足を Q とする。→AQ を →AB と →AC で表せ。
解
→AQ=α→AB+β→AC
と置く。
→OQ=→AQ–→AO=α→AB+β→AC–→AO
より、
0=→OQ⋅→AB=(α→AB+β→AC–→AO)⋅→AB=3α+2β+1
0=→OQ⋅→AC=(α→AB+β→AC–→AO)⋅→AC=2α+6β–4
∴α=−1,β=1
ゆえに、
→AQ=−→AB+→AC
解説
CGで答えを確認
下記↓のアニメーションの確認でも確かに →AQ=−→AB+→AC は確認できます。
(回転自体にはあまり意味は無いですが、垂線 OQ を立体的にイメージできるための前振りです。)
内積ゼロ
OQ は平面への垂線なので、平面を構成する2つの方向ベクトル →AB と →AC に垂直です。従って、内積ゼロを使っています。
外積でも確かめられる
→AB と →AC の外積は

(−3,1,−2) なので、このベクトルと平面 H のベクトル方程式
(xyz)=(313)+s(11−1)+t(1−1−2)
との内積を取ることにより、平面 H の方程式は
3x−y+2z=14
を得ます(両辺 −1 倍しています)。
また、直線 OQ のベクトル方程式は
(xyz)=q(3−12)
より、平面の式に代入して、
q=1
を得ますから、
Q(3,−1,2)
であることが分かり、確かに
→AQ=−→AB+→AC
が成り立っていることが分かります。
外積は↓の記事で解説しています。
また、垂線の足という観点では、↓の記事も理解に幅を持たせるうえで参考になります。
(3) →AR=r→AC (r は非負の実数) を満たす点 R の存在証明
(3) 領域 K 上の点 P に対して、線分 QP 上の点で →AR=r→AC (r は非負の実数) を満たす点 R が存在することを示せ。
解説に示すアニメーションを見れば題意を満たすことはほぼ自明なのですが、それをどのようにして定式化するかです。それは、点 R は直線 AC と QP の交点であることを用います。
解
点 R は線分 QP 上の点なので、
→AR=ω→AP+(1−ω)→AQ(0≤ω≤1)
と表せる。よって、
→AR=ω(s→AB+t→AC)+(1−ω)(−→AB+→AC)=(sω+ω−1)→AB+(tω−ω+1)→AC
ここで、点 R は AC 上にあるので、
sω+ω−1=0
∴ω=1s+1(∵s>0)
よって、
→AR=s+ts+1→AC
ここで、
r=s+ts+1>0(∵s,t>0)
と置けるから、証明終わり。
解説
点 P が領域 K 内で彷徨っています。領域 K 内に P がいる限り、点 R は点 A よりも C 側にいるのはほぼ自明です。
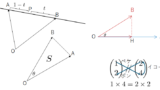
(4) 距離の最小問題
(4) 領域 K において原点 O からの距離が最小となる点 S の座標を求めよ。
上のアニメーションより、領域 K 内のいかなる点 P よりも点 R の方が点 O から近いです。そして点 R の中でさらに最小となるのは、QR と AC が垂直の場合です。
解
OP2=OQ2+QP2
より、OP が最小になるのは QP が最小のとき。
(3)より QR≤QP なので、QR が最小になる場合を考えればよい。
これは、QR と AC が垂直になる場合であり、その点が S だから、
→AS=γ→AC,γ≥0
と置いて、
0=→QS⋅→AC=(→AS−→AQ)⋅→AC=(γ→AC+→AB−→AC)⋅→AC=6γ+2−6
∴γ=23
ゆえに
S(113,13,53)
解説
γ=23 の状態は下記↓です。

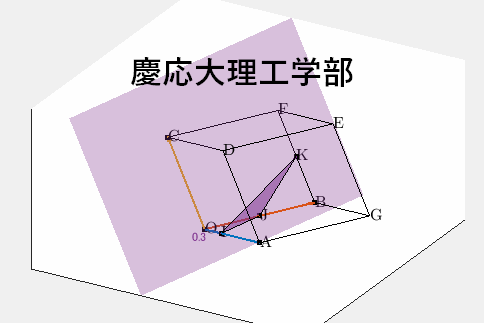
慶応義塾大学・理工学部
平行六面体 OAGB−CDEF において、→OA=→a, →OB=→b, →OC=→c とおき、|→a|=1, |→b|=2, |→c|=2, →a⋅→b=1, →a⋅→c=−1, →b⋅→c=0 とする。
(1) 三角形 OAB の面積は [ ] である。頂点 C から3点 O, A, B を通る平面に垂線を下ろし、この平面との交点を H とすると、→CH=[ ]→a+[ ]→b−→c である。四面体 OABC の体積は [ ] である。
辺 OA をt:1−t に内分する点を I、辺 OB の中点を J、辺 BF の中点を K とする。ただし、0<t<1 とする。
(2) →JI⋅→JK=[ ] であり、三角形 IJK の面積は [ ] である。
(3) 3点 I, J, K を通る平面が辺 DE と共有点を持つのは、[ ]≤t<1 のときである。
六面体は下記↓のようなイメージです。

(1) 三角形の面積問題、垂直問題からの体積問題
(1) 三角形 OAB の面積は [ ] である。頂点 C から3点 O, A, B を通る平面に垂線を下ろし、この平面との交点を H とすると、→CH=[ ]→a+[ ]→b−→c である。四面体 OABC の体積は [ ] である。
三角形の面積 S には公式があります。
S=12√|→a|2|→b|2−(→a⋅→b)2

復習はこちらの記事↓で。三角形の面積部分への直接リンクはこちら。
垂直は内積ゼロ。
これらが出れば、体積は求められます。
解
△OAB の面積
△OAB=12√|→a|2|→b|2−(→a⋅→b)2=12√1222−12=√32
→CH
→OH=s→a+t→b
と置くと、
→CH=→OH–→OC=s→a+t→b–→c
より、
0=→CH⋅→a=s|→a|2+t→a⋅→b−→a⋅→c=s+t+1
0=→CH⋅→b=s→a⋅→b+t|→b|2−→b⋅→c=s+4t
∴s=−43,t=13
よって、
→CH=−43→a+13→b−→c
四面体 OABC の体積
|→CH|2=(−43→a+13→b−→c)2=169|→a|2+19|→b|2+|→c|2−24313→a⋅→b−213→b⋅→c+243→a⋅→c=169+49+4−89−83=83
より、四面体 OABC の体積を V と置くと、
V=13×△OAB×|→CH|=13×√32×2√2√3=√23
解説
上記の解をアニメーションで確認します。おおよそこのようなイメージを持ちながら解法が思いつくようになるとGoodです。
(2) 辺 OA をt:1−t に内分する点問題
辺 OA をt:1−t に内分する点を I、辺 OB の中点を J、辺 BF の中点を K とする。ただし、0<t<1 とする。
(2) →JI⋅→JK=[ ] であり、三角形 IJK の面積は [ ] である。
点 I は辺 OA をt:1−t に内分する点なので、素直に →OI=t→OA です。その他、→OJ=12→OB、→OK=→OB+12→OC です。

内分点問題はこちらの記事↓で復習できます。該当箇所に直接飛ぶリンクはこちら。
解
→JI=t→a–12→b
→JK=(→b+12→c)−12→b=12(→b+→c)
より、
→JI⋅→JK=(t→a–12→b)⋅12(→b+→c)=12(t→a⋅→b+t→a⋅→c−12|→b|2−12→b⋅→c)=−1
よって、
△IJK=12√|→JI|2|→JK|2−(→JI⋅→JK)2=⋯=12√2t2−2t+1
解説
全体イメージを示すとこのよう↓です。
ここで、→JI⋅→JK=−1 と、t によらない定数になったことを振り返りましょう。アニメーションの中で真横から見たシーンがありました。

このとき、t の値が変化しても、I から直線 KJ に下した垂線の足 I′ は変化しませんでした。これが、→JI⋅→JK=−1 と、t によらない定数になった理由です。
頭の中でこのようなシミュレーションをすることは難しいので、逆に、内積が t によらない定数になったということは、このような状況なのだと理解するとよいです。
(3) 平面と線分との共有点
(3) 3点 I, J, K を通る平面が辺 DE と共有点を持つのは、[ ]≤t<1 のときである。
どのように立式してよいかをイメージするため、まずはアニメーションから見てみましょう。
アニメーション
3点 I, J, K を通る平面は紫です。右下の紫の数字は t の値です。アニメーションの最初のコマは t=0.3 ということです。
さてまずはこのとき、平面は辺と共有点を持つでしょうか。コマを進めると平面の真横から見た図になります。

図より、共有点を持っていないことが分かります。
そして t の値を大きくしていき、t=1 となったところでまた平面を横から見ています。

今度はぎりぎり、点 E で以って共有しています。ただし、問題文では 0<t<1 となっていることに注意が必要です。
では、共有点を有するもう一つのぎりぎりの t はいくつでしょうか。コマを進めると今度は点 D と共有点を持つところで止まり、平面を真横から見ています。

このとき、t=13 です。
従って答えは 13≤t<1 です。問題はこれをどのように定式化すればよいか、です。
それは、共有点 P は平面上の点でもあり、辺上の点でもある、ということを定式化することです。
解
平面 IJK と辺 DE の共有点を P とすると、P が平面 IJK 上にあることから、
→OP=→OJ+p→JI+q→JK=12→b+p(t→a−12→b)+q12(→b+→c)=tp→a+12(1−p+q)→b+12q→c
と表せる。一方、P は辺 DE 上の点でもあるので、
→OP=→OD+k→DE=→a+→c+k→b(0≤k≤1)
と表せる。
ここで →a, →b, →c は一次独立なので、
tp=112(1−p+q)=k12q=1
0<t より(1)から p=1t。
また、(3)から q=2。
これを(2)に代入し、0≤k≤1 に注意すると、
0≤k=12(3−1t)≤1
∴1≤1t≤3
0<t<1 より、
13≤t<1
京都大学 文系
四面体 OABC が次を満たすとする。
OA=OB=OC=1,∠COA=∠COB=∠ACB,∠AOB=90∘
このとき、四面体 OABC の体積を求めよ。
方針検討
OA=OB=1, ∠AOB=90∘ から、A, B は (1,0,0), (0,1,0) に配置できます。
そして、∠COA=∠COB から点 C は (p,p,〇) に位置することも分かります。
まずはこれらのイメージを立体図アニメーションで確認します。
そして、OC=1 から点 C の座標が
C(p,p,√1−2p2)
と置けます。
残る条件は、∠ACB=∠COA=∠COB です。このイメージは、
∠COA=∠COB=θ1 を変えたら ∠ACB=θ2 が変わる
というイメージを持つことです。こんな感じ↓で。
このイメージが持てればあとは θ1, θ2 を何らかの方法で表し、両者を等しいと置けばよいですね。何らかの方法とは、余弦定理を使うか、同じことですがベクトルの内積を使うかです。余弦定理については↓の記事を見てください。
解
OA=OB=1, ∠AOB=90∘ から、
A(1,0,0),B(0,1,0)
と置ける。
∠COA=∠COB より、点 C の x と y 座標は等しくこれを p と置く。また対称性から z>0 側でのみ考えて一般性を失わない。そして、OC=1 より、
C(p,p,√1−2p2)
と置ける。
∠COA=∠COB=θ1∠ACB=θ2
と置くと、
cosθ1=→a⋅→c|→a||→c|=(100)⋅(pp√1−2p2)1×1=p
一方、
cosθ2=→CA⋅→CB|→CA||→CB|=(1−p−p−√1−2p2)⋅(−p1−p−√1−2p2)|(1−p−p−√1−2p2)|⋅|(−p1−p−√1−2p2)|=−p(1−p)−p(1−p)+(1−2p2)(1−p)2+p2+(1−2p2)=1−2p2(1−p)
ここで θ1=θ2 なので (1)=(2) として、
p=1−2p2(1−p)2p2−4p+1=0p=2±√22
ここで p=cosθ1≤1 より、
p=2−√22
よって、求める体積 V は、
V=1312√1−2p2=⋯=16√2√2−2
まとめ
難関大学の入試問題のうち、空間ベクトルを取り上げました。ベクトルは図形の問題を単なる計算問題に落とし込めるところが非常に面白いです。そのため直線や平面をベクトルで表現します。ここの問題がスラスラ解けることを目標に、今一度↓の記事の基礎部分を復習してもらえると幸甚です。





コメント