ベクトル方程式が立てられれば軌跡方程式へは一発変換できます。それには法線ベクトルと内積を取ります。法線ベクトルを求めるには【外積】を使います。高校では習わない裏技ですが、知っていると見通しがグッとよくなります。
外積の公式
ベクトル $\overrightarrow{a}=(x_1,y_1,z_1)$ とベクトル $\overrightarrow{b}=(x_2,y_2,z_2)$ の外積は、次のように求められます。
すなわち、各ベクトルを2つずつ横に並べて書き、両端を消します。そして左端からたすき掛けを行い、新しいベクトルの成分とします。具体的に今回の例だと次のようになります。
外積を $\overrightarrow{c}$ と書くと、次のように表現します。
$$\overrightarrow{c} = \overrightarrow{a}\times\overrightarrow{b}$$
外積の意味するところ
内積はスカラーでしたが外積はベクトルです。ベクトルには向きと大きさがあります。それぞれの意味を今回のベクトルを例に見ていきます。今回のベクトルを外積の式の形で再掲すると、
$$\overrightarrow{c} = \overrightarrow{a}\times\overrightarrow{b}$$
成分表示では、
$$\begin{pmatrix}3\\3\\3\end{pmatrix} = \begin{pmatrix}-1\\2\\-1\end{pmatrix}\times\begin{pmatrix}-2\\1\\1\end{pmatrix}$$
です。
向き：両方に垂直
外積である $\begin{pmatrix}3\\3\\3\end{pmatrix}$ は元の2つのベクトル $\begin{pmatrix}-1\\2\\-1\end{pmatrix}$、$\begin{pmatrix}-2\\1\\1\end{pmatrix}$ の両方に垂直です。それは内積を取れば確かめられます。
$$\begin{pmatrix}3\\3\\3\end{pmatrix}\cdot\begin{pmatrix}-1\\2\\-1\end{pmatrix}=0$$
$$\begin{pmatrix}3\\3\\3\end{pmatrix}\cdot\begin{pmatrix}-2\\1\\1\end{pmatrix}=0$$
です。
そして、上下の向きについては、$\overrightarrow{a}=\begin{pmatrix}-1\\2\\-1\end{pmatrix}$ から $\overrightarrow{b}=\begin{pmatrix}-2\\1\\1\end{pmatrix}$ に右ねじを回して進む向きです。下図のようになります。
下記↓のアニメーションは、この先の「外積の使いどころ」で出てくる座標を先走って書いていますが、点 $\mathrm{A}\, (3,0,3)$, 点 $\mathrm{B}\, (2,2,2)$, 点 $\mathrm{C}\, (1,1,4)$ として平面を形成しており、その平面のベクトル方程式は、
$$\begin{pmatrix}x\\y\\z\end{pmatrix} = \begin{pmatrix}3\\0\\3\end{pmatrix} + s\begin{pmatrix}-1\\2\\-1\end{pmatrix} + t\begin{pmatrix}-2\\1\\1\end{pmatrix}$$
です。ここで、
$$\overrightarrow{a}=\overrightarrow{\mathrm{AB}}=\begin{pmatrix}-1\\2\\-1\end{pmatrix}$$
$$\overrightarrow{b}=\overrightarrow{\mathrm{AC}}=\begin{pmatrix}-2\\1\\1\end{pmatrix}$$
$$\overrightarrow{a}\times\overrightarrow{b}=\begin{pmatrix}3\\3\\3\end{pmatrix}/\! /\begin{pmatrix}1\\1\\1\end{pmatrix}=\overrightarrow{n}$$
であり、確かに下記のように $\overrightarrow{n}$ は $\overrightarrow{a}$ と $\overrightarrow{b}$ の両方に垂直です。
大きさ：平行四辺形の面積
$\overrightarrow{c}$ の大きさは、$\overrightarrow{a}$ と $\overrightarrow{b}$ で張る平行四辺形の面積です。下図のようになります。
すなわち、
$$\overrightarrow{c}=\begin{pmatrix}3\\3\\3\end{pmatrix}$$
の大きさである
$$|\overrightarrow{c}|=\left|\begin{pmatrix}3\\3\\3\end{pmatrix}\right|=3\sqrt{3}$$
が、$\overrightarrow{a}$ と $\overrightarrow{b}$ が張る平行四辺形の面積だと主張しています。練習問題がてら、自身で確かめてみてください。ヒントは、余弦定理か内積の定義を使えば $\overrightarrow{a}$ と $\overrightarrow{b}$ のなす角は $60^\circ$ であることが分かります。
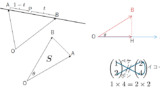
外積の使いどころ：ベクトル方程式から軌跡方程式への変換
問題風にしてやりたいことを確認
問題風にすると次のようです。
次の平面のベクトル方程式を軌跡方程式（$ax+by+cz=d$ の形）にせよ。
$$\begin{pmatrix}x\\y\\z\end{pmatrix} = \begin{pmatrix}3\\0\\3\end{pmatrix} + s\begin{pmatrix}-1\\2\\-1\end{pmatrix} + t\begin{pmatrix}-2\\1\\1\end{pmatrix}$$
平面のベクトル方程式については下記↓の記事でイメージをつかむことができます。
外積で内積を取る
先に求めたように、ベクトル $\begin{pmatrix}-1\\2\\-1\end{pmatrix}$ と $\begin{pmatrix}-2\\1\\1\end{pmatrix}$ の外積は $\begin{pmatrix}3\\3\\3\end{pmatrix}$ です。ここでは同じ向きである
$$\overrightarrow{n}=(1,1,1)$$
を用いていきます。
解
$$\begin{pmatrix}x\\y\\z\end{pmatrix} = \begin{pmatrix}3\\0\\3\end{pmatrix} + s\begin{pmatrix}-1\\2\\-1\end{pmatrix} + t\begin{pmatrix}-2\\1\\1\end{pmatrix}$$
に対してベクトル $\begin{pmatrix}1\\1\\1\end{pmatrix}$ で内積を取ることにより、
$$x+y+z=6$$
を得る。
解説
ここでのミソは、ベクトル $\begin{pmatrix}1\\1\\1\end{pmatrix}$ で内積を取ることにより媒介変数 $s$, $t$ が掛かっているベクトルが消えてなくなるということです。つまり、
\begin{eqnarray}
\begin{pmatrix}1\\1\\1\end{pmatrix}\cdot\begin{pmatrix}-1\\2\\-1\end{pmatrix} &=& 0\\
\begin{pmatrix}1\\1\\1\end{pmatrix}\cdot\begin{pmatrix}-2\\1\\1\end{pmatrix} &=& 0
\end{eqnarray}
ということです。
そしてもちろん、
- 左辺の $x+y+z$ は $\begin{pmatrix}1\\1\\1\end{pmatrix}\cdot\begin{pmatrix}x\\y\\z\end{pmatrix}$ のこと
- 右辺の $6$ は $\begin{pmatrix}1\\1\\1\end{pmatrix}\cdot\begin{pmatrix}3\\0\\3\end{pmatrix}$ のこと
です。
物理でよく出てくる
外積という概念は物理でよく出てきます。主には大学に入ってからの物理ですが、高校の範囲でも、表立っては主張しませんが実は外積、というものがいくつかあります。その代表は力のモーメントです。なお、外積の演算記号は $\times$ です。
力のモーメント
力のモーメント $\overrightarrow{N}$ は次の式で表されます。
$$\overrightarrow{N} = \overrightarrow{r}\times\overrightarrow{F}$$
ここで、$\overrightarrow{r}$ は作用点の位置ベクトルを、$\overrightarrow{F}$ は力を表します。
力のモーメントの問題は24年度の共通テストでも出ました。↓の記事で解説しています。
ケプラーの第二法則
太陽の周りをまわる惑星は楕円軌道を描きますが、このとき太陽から見た惑星の位置 $\overrightarrow{r}$ と速度 $\overrightarrow{v}$ の外積 $\overrightarrow{L}$ は一定になります。
$$\overrightarrow{L} = \overrightarrow{r}\times\overrightarrow{v} = \mathrm{const.}$$
この $\overrightarrow{L}$ は角運動量という物理量ですが、これが保存します。面積速度一定の法則とも言います。イメージで捉えると下記↓のようです。
まとめ
外積を使って平面の方程式を求めました。外積は高校では習わないですが、使えると空間ベクトルの見通しが非常に良くなるので使えると強いです。
コメント