難関校では空間図形の問題がよく出ます。空間図形は慣れないと頭から煙が出そうになりますよね。空間図形が頭の中で自由自在の角度から見られるようになれば、難しい空間図形も難なく解けるようになります。ここのアニメーションを繰り返し見ることにより自分の頭の中でも図形が泳ぐようになってもらえると幸いです。
問題1:正四角錐を底面の角から切断
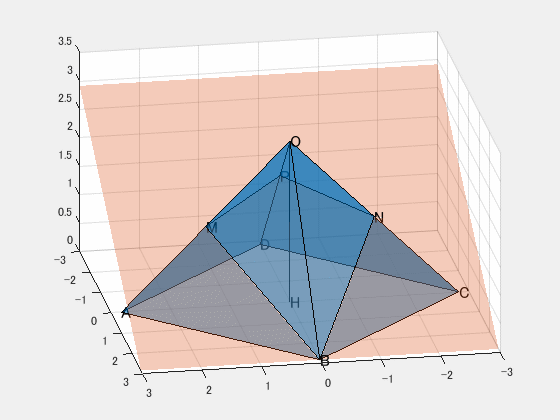
図のように、すべての辺の長さが $4$ cmの正四角錐 $\mathrm{O-ABCD}$ がある。辺 $\mathrm{OA}$, 辺 $\mathrm{OC}$ の中点をそれぞれ $\mathrm{M}$, $\mathrm{N}$ とする。また、点 $\mathrm{O}$ から底面 $\mathrm{ABCD}$ に垂線 $\mathrm{OH}$ をひく。この正四角錐を $3$ 点 $\mathrm{B}$, $\mathrm{M}$, $\mathrm{N}$ を通る平面で切ったとき、

(1) $\mathrm{OH}$ の長さを求めよ。
(2) 切り口の面積を求めよ。
(3) $2$ つに分けた立体のうち、点 $\mathrm{O}$ を含む方の立体の体積を求めよ。
(23年 東海高校)
平面で切るイメージは浮かびますか?この図のイメージです。
(2)の切り口の面積は、$\mathrm{MN}$ と $\mathrm{BP}$ の長さが求まれば求められます。
そして、(3)は(2)を利用して求めます。
しかし、実は別解の方がより基本に忠実だろうと思います。
(3)で、底面 $\mathrm{BMPN}$ に対する高さを求める際には下図のように切って考えます。
解(1). $\mathrm{OH}$ の長さ
$\triangle\mathrm{AHB}$ は直角二等辺三角形なので、$\mathrm{AH} = 2\sqrt{2}\mathrm{cm}$。
さらに、$\triangle\mathrm{OAH}$ は直角三角形なので、三平方の定理より、
\begin{eqnarray}
\mathrm{OH}^2 &=& 4^2-(2\sqrt{2})^2\\
&=& 8\\
\therefore\; \mathrm{OH} &=& 2\sqrt{2}
\end{eqnarray}

解(2). 切り口の面積
切り口の図形は下図。よって、$\mathrm{MN}$ と $\mathrm{BP}$ の長さが求まれば面積は求まる(辺 $\mathrm{OD}$ と切断平面との交点を $\mathrm{P}$ と置いた)。

$\mathrm{MN}$ の長さは $\mathrm{AC}$ の半分なので、$\mathrm{MN}=2\sqrt{2}$。
$\mathrm{BP}$ の長さを求める。
まず、点 $\mathrm{P}$ は $\mathrm{OD}$ を $3$ 等分する。なぜなら、下図より、
$\triangle\mathrm{OHQ}\unicode[sans-serif]{x223D}\triangle\mathrm{OMP}$ で、$\mathrm{OM}=\mathrm{MH}$より、$\mathrm{OP}=\mathrm{PQ}$。
$\triangle\mathrm{DBP}\unicode[sans-serif]{x223D}\triangle\mathrm{DHQ}$ で、$\mathrm{DH}=\mathrm{HB}$ より、$\mathrm{DQ}=\mathrm{QP}$。
よって、$\mathrm{OP}=\mathrm{PQ}=\mathrm{QD}$。

下図の直角三角形 $\mathrm{BPI}$ に着目をする( $\mathrm{P}$ から $\mathrm{BD}$ に下した垂線の足を $\mathrm{I}$ と置いた)。ここで、
$\mathrm{OH}=2\sqrt{2}$ より、$\mathrm{PI}=\displaystyle\frac{2}{3}\mathrm{OH}=\displaystyle\frac{4\sqrt{2}}{3}$
$\mathrm{BH}=2\sqrt{2}$ より、$\mathrm{HI}=\displaystyle\frac{1}{3}\mathrm{BH}=\displaystyle\frac{2\sqrt{2}}{3}$
である。

\begin{eqnarray}
\mathrm{BP}^2 &=& \left(2\sqrt{2}+\frac{2\sqrt{2}}{3}\right)^2+\left(\frac{4\sqrt{2}}{3}\right)^2\\
&=& \left(\frac{4}{3}\sqrt{2}\right)^2\times 5\\
\therefore\; \mathrm{BP} &=& \frac{4}{3}\sqrt{2}\times\sqrt{5}\\
&=& \frac{4}{3}\sqrt{10}
\end{eqnarray}
($\rightarrow\;\mathrm{BP}^2$ の計算を楽に行う:解説1)
よって求める面積 $S$ は、
\begin{eqnarray}
S &=& \frac{1}{2}\cdot\mathrm{MN}\cdot\mathrm{BP}\\
&=& \frac{1}{2}\cdot 2\sqrt{2}\cdot\frac{4}{3}\sqrt{10}\\
&=& \frac{8}{3}\sqrt{5}
\end{eqnarray}
($\rightarrow$ 面積の求め方はマスターしよう:解説2)
解(3). 切断上側の体積
解答としては解説5に示す方がシンプルです。シンプルゆえにより発想力が必要なので、ここではまずはあまり発想せずに解ける方法で解きます。その分、計算はしんどいです。
解
$\mathrm{O}$ から $\mathrm{BP}$ に下した垂線の足をJと置き、平面 $\mathrm{OBD}$ で切る。


このとき、点 $\mathrm{B}$ を原点として $xy$ 平面に描画すると点 $\mathrm{O}$, $\mathrm{B}$, $\mathrm{D}$, $\mathrm{P}$ の座標は(1)(2)の結果から下図のようになる。
さらに、直線 $\mathrm{BP}$ と直線 $\mathrm{OJ}$ は垂直に交わることからそれぞれの直線の式は
\begin{eqnarray}
\left\{\begin{array}{l}
y&=&\displaystyle\frac{1}{2}x\\
y&=&-2(x-2\sqrt{2})+2\sqrt{2}
\end{array}
\right.
\end{eqnarray}
($\rightarrow$ 直線の式を楽に求める:解説3)
$$\therefore\; \mathrm{J}\left(\frac{12}{5}\sqrt{2},\,\frac{6}{5}\sqrt{2}\right)$$

$\mathrm{J}$ が求まったので $2$ 点 $\mathrm{O}$, $\mathrm{J}$ の座標から、
\begin{eqnarray}
\mathrm{OJ}^2 &=& \left(\frac{12}{5}\sqrt{2}-2\sqrt{2}\right)^2+\left(\frac{6}{5}\sqrt{2}-2\sqrt{2}\right)^2\\
&=& \left(\frac{2}{5}\sqrt{2}\right)^2\times 5\\
\therefore\;\mathrm{OJ} &=& \frac{2}{5}\sqrt{2}\times\sqrt{5}\\
&=& \frac{2}{5}\sqrt{10}
\end{eqnarray}
($\rightarrow\;\mathrm{OJ}^2$ の計算を楽に行う:解説4)
従って求める体積 $V$ は、
\begin{eqnarray}
V &=& \frac{1}{3}\cdot S\cdot\mathrm{OJ}\\
&=& \frac{1}{3}\cdot \frac{8}{3}\sqrt{5}\cdot\frac{2}{5}\sqrt{10}\\
&=& \frac{16}{9}\sqrt{2}
\end{eqnarray}
($\rightarrow$ 別解_底面の捉え方を変える:解説5)
解説1. $\mathrm{BP}^2$ の計算を楽に行う
次のように式変形できると楽です。
\begin{eqnarray}
\mathrm{BP}^2 &=& \left(2\sqrt{2}+\frac{2\sqrt{2}}{3}\right)^2+\left(\frac{4\sqrt{2}}{3}\right)^2\\
&=& \left(\frac{8\sqrt{2}}{3}\right)^2+\left(\frac{4\sqrt{2}}{3}\right)^2\\
&=& \left(\frac{4\sqrt{2}}{3}\right)^2\times (2^2+1^2)\\
&=& \left(\frac{4\sqrt{2}}{3}\right)^2\times 5
\end{eqnarray}
因数分解を利用しています。このテクニックもちょっとしたことですが、使えると計算が楽に正確にできる場面が結構あります。
解説2. 面積の求め方はマスターしよう
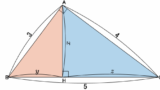
解答の計算は、暗黙のうちに四角形 $\mathrm{BMPN}$ を2つの三角形に分割して計算しています。

つまり、この絵のように分割すると、
\begin{eqnarray}
\mathrm{BMPN} &=& \triangle\mathrm{PMN}+\triangle\mathrm{BMN}\\
&=& \frac{1}{2}\cdot\mathrm{MN}\cdot\mathrm{PR}+\frac{1}{2}\cdot\mathrm{MN}\cdot\mathrm{BR}\\
&=& \frac{1}{2}\cdot\mathrm{MN}\cdot(\mathrm{PR}+\mathrm{BR})\\
&=& \frac{1}{2}\cdot\mathrm{MN}\cdot\mathrm{PB}
\end{eqnarray}
となり、解答の計算になります。このテクニックは非常によく使います。
↓の記事の「パターン0」も同様の考え方を使っています。同じ発想を違う問題で眺めるのは非常に意味があるのでこちらもぜひ見てください。
解説3. 直線の式: $y=-2(x-2\sqrt{2})+2\sqrt{2}$ を楽に求める
直線 $\mathrm{BP}$ の式は $\mathrm{P}$ の座標からすぐに求められると思いますが、直線 $\mathrm{OJ}$ の式を求めるのが難しいと感じる人が多いと思います。ポイントは2つあり、
- 直線 $\mathrm{OJ}$ の傾きはいくつか?
- 傾きが分かったらすぐに直線の式が書けるか?
です。
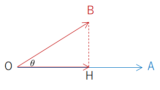
直線 $\mathrm{OJ}$ の傾きはいくつか?
$\mathrm{BP}$ の傾きが $\displaystyle\frac{1}{2}$ であり、それに垂直なので、傾きは $-2$ です。
これについては↓の記事で詳しく解説しているので参考にしてください。高校生向けに書いた記事なので、この中の「傾きの積を利用」だけ見ればよいです。
傾きが分かったらすぐに直線の式が書けるか?
傾きと通る1点が分かれば直線の式は一行で書けます。公式風に書くと次のようです。
傾きが $a$ で点(〇, □)を通る直線の式は、
$$y=a(x-〇)+□$$
ちょっとしたことですが、これを知っていると直線の式を楽に求められます。
これも↓の記事で詳しく解説しています。
解説4. $\mathrm{OJ}^2$ の計算を楽に行う
これも先の $\mathrm{BP}^2$ の計算同様、次のように式変形すると楽です。
\begin{eqnarray}
\mathrm{OJ}^2 &=& \left(\frac{12}{5}\sqrt{2}-2\sqrt{2}\right)^2+\left(\frac{6}{5}\sqrt{2}-2\sqrt{2}\right)^2\\
&=& \left(\frac{2}{5}\sqrt{2}\right)^2+\left(\frac{4}{5}\sqrt{2}\right)^2\\
&=& \left(\frac{2}{5}\sqrt{2}\right)^2\times (1^2+2^2)\\
&=& \left(\frac{2}{5}\sqrt{2}\right)^2\times 5
\end{eqnarray}
解説5. 体積 $V$ の別解
この問題では(2)で立体の底面の面積を求めさせているので(3)の体積は高さ $\mathrm{OJ}$ を求めることにより算出することでよいのだろうと思いますが、実は底面積も高さも両方とも出すことなく体積は求められます。
それにはこの立体を $\mathrm{OBD}$ で半分に割り、底面を $\mathrm{OCD}$ と捉え直します。次のアニメーションを見てください。


$$\triangle\mathrm{ONP} = \frac{1}{6}\triangle\mathrm{OCD}$$
なので、体積も $\displaystyle\frac{1}{6}$ となります。
ここで、元の体積 $V_{\mathrm{O-ABCD}}$ は、
\begin{eqnarray}
V_{\mathrm{O-ABCD}} &=& \frac{1}{3}\cdot\left(\frac{1}{2}\cdot\mathrm{AC}\cdot\mathrm{BD}\right)\cdot\mathrm{OH}\\
&=& \frac{1}{6}\cdot 4\sqrt{2}\cdot 4\sqrt{2}\cdot 2\sqrt{2}\\
&=& \frac{32}{3}\sqrt{2}
\end{eqnarray}
よって、求める体積 $V$ は、
\begin{eqnarray}
V &=& \frac{1}{6}\cdot V_{\mathrm{O-ABCD}}\\
&=& \frac{1}{6}\cdot\frac{32}{3}\sqrt{2}\\
&=& \frac{16}{9}\sqrt{2}
\end{eqnarray}
となり、解答に示した値と一致します。
まとめ
正四角錐を底面の角と隣の辺の中点を結ぶ平面で切断しました。
まず、立体の高さは三平方の定理から簡単に求められ、従って全体の体積はすぐに求められることを理解しましょう。
その後は設問の誘導に従って解いていけばよいですが、このように底面の捉え方を変えることで立体の体積比がすぐに分かる場合があること、そしてこの場合はそれが $\displaystyle\frac{1}{6}$ であることを経験できたのはよいことだと思います。
$\displaystyle\frac{1}{6}$ であることは次の式が立体とともに頭に浮かぶようになるとよいです。
$$\frac{1}{6}=\frac{1}{2}\cdot\frac{1}{3}$$
$\displaystyle\frac{1}{2}$ は $\mathrm{ON}=\displaystyle\frac{1}{2}\mathrm{OC}$ を、$\displaystyle\frac{1}{3}$ は $\mathrm{OP}=\displaystyle\frac{1}{3}\mathrm{OD}$ を表しています。
問題2:正四角錐を底面の辺から切断
図のように、$1$ 辺がすべての $8\mathrm{cm}$ の正四角錐 $\mathrm{OABCD}$ があり、辺 $\mathrm{OB}$ の中点を $\mathrm{P}$ とする。この正四角錐を $3$ 点 $\mathrm{A}$, $\mathrm{D}$, $\mathrm{P}$ を通る平面で切ったとき、

(1) 正四角錐 $\mathrm{OABCD}$ の体積を求めよ。
(2) 切り口の図形の面積を求めよ。
(3) $2$ つに分けた立体のうち、点 $\mathrm{O}$ を含む方の立体の体積を求めよ。
(21年 東海高校)
(2)の問題にある切り口の図形の形はイメージできるでしょうか。このイメージです。
また、(3)の立体は、問題1でも見たように半分に分けることで楽に求められます。ただし、出題者の意図は(2)との連続性から切り口を底面と見た高さを求めさせることにあると思いますので、ここでも解と別解を示します。
(3)で、底面 $\mathrm{ADQP}$ に対する高さを求める際には下図のように切って考えます。
解(1). $\mathrm{OABCD}$ の体積
点 $\mathrm{O}$ から底面 $\mathrm{ABCD}$ に下した垂線の足を $\mathrm{H}$ と置くと、$\mathrm{OH}$ の長さは明らかに問題1の $2$ 倍なので、
$$\mathrm{OH}=4\sqrt{2}$$
また、底面 $\mathrm{ABCD}$ の面積は $8\times8=64$ なので、求める体積 $V$ は、
\begin{eqnarray}
V &=& \frac{1}{3}\cdot 64\cdot 4\sqrt{2}\\
&=& \frac{256}{3}\sqrt{2}
\end{eqnarray}
解(2). 切り口の面積
切り口の図形は下図であり、四角形 $\mathrm{ADQP}$ は台形である(辺 $\mathrm{OC}$ と切断平面との交点を $\mathrm{Q}$ と置いた)。

$\mathrm{AD}$ の長さは問題文より、$8$。
$\mathrm{PQ}$ の長さは $\mathrm{BC}$ の半分なので、$4$。
従って、あとは台形の高さを求めればよい。
下図左に示すように $\mathrm{AP}$ は正三角形 $\mathrm{OAB}$ を半分に分けており$\triangle\mathrm{APB}$ が直角三角形であることに注意すると、その長さは $4\sqrt{3}$。

さらに同図右より $\mathrm{PR}$ ($\mathrm{R}$ は $\mathrm{P}$ から $\mathrm{AD}$ に下した垂線の足)の長さは直角三角形 $\mathrm{PRA}$ に着目することにより、
\begin{eqnarray}
\mathrm{PR}^2 &=& \mathrm{PA}^2-\mathrm{RA}^2\\
&=& (4\sqrt{3})^2-2^2\\
&=& 44\\
\therefore\; \mathrm{PR} &=& 2\sqrt{11}
\end{eqnarray}
よって、求める面積 $S$ は、
\begin{eqnarray}
S &=& \frac{1}{2}\cdot (\mathrm{PQ}+\mathrm{AD})\cdot\mathrm{PR}\\
&=& \frac{1}{2}\cdot (4+8)\cdot 2\sqrt{11}\\
&=& 12\sqrt{11}
\end{eqnarray}
解(3). 切断上側の体積
ここも問題1と同様に、解説2の方がシンプルです。
解
$\mathrm{AD}$ と $\mathrm{BC}$ の中点をそれぞれ $\mathrm{S}$, $\mathrm{T}$ と置き、平面 $\mathrm{OST}$ で切る($\mathrm{PQ}$ と切断面の交点を $\mathrm{U}$ と置いた)。さらに $\mathrm{O}$ から平面 $\mathrm{ADQP}$ に下した垂線の足を $\mathrm{J}$ と置く。


このとき、点 $\mathrm{S}$ を原点として $xy$ 平面に描画すると点 $\mathrm{O}$, $\mathrm{S}$, $\mathrm{T}$, $\mathrm{U}$ の座標は(1)(2)の結果から下図のようになる。
さらに、直線 $\mathrm{SU}$ と直線 $\mathrm{OJ}$ は垂直に交わることからそれぞれの直線の式は
\begin{eqnarray}
\left\{ \begin{array}{l}
y=\displaystyle\frac{\sqrt{2}}{3}x\\
y=-\displaystyle\frac{3}{\sqrt{2}}(x-4)+4\sqrt{2}
\end{array}
\right.
\end{eqnarray}
($\rightarrow$ 直線の式を楽に求める:問題1の解説3)
$$\therefore\; \mathrm{J}\left(\frac{60}{11},\frac{20}{11}\sqrt{2}\right)$$

$\mathrm{J}$ が求まったので2点 $\mathrm{O}$, $\mathrm{J}$ の座標から、
\begin{eqnarray}
\mathrm{OJ}^2 &=& \left(\frac{60}{11}-4\right)^2+\left(\frac{20}{11}\sqrt{2}-4\sqrt{2}\right)^2\\
&=& \left(\frac{8}{11}\right)^2\times 22\\
\therefore\;\mathrm{OJ} &=& \frac{8}{11}\sqrt{22}
\end{eqnarray}
($\rightarrow\;\mathrm{OJ}^2$ の計算を楽に行う:解説1)
従って求める体積 $V$ は、
\begin{eqnarray}
V &=& \frac{1}{3}\cdot S\cdot\mathrm{OJ}\\
&=& \frac{1}{3}\cdot 12\sqrt{11}\cdot\frac{8}{11}\sqrt{22}\\
&=& \frac{1}{3}\cdot 12\cancel{\sqrt{11}}\cdot\frac{8}{\cancel{11}}\cancel{\sqrt{11}}\sqrt{2}\\
&=& 32\sqrt{2}
\end{eqnarray}
($\rightarrow$ 別解_底面の捉え方を変える:解説2)
解説1. $\mathrm{OJ}^2$ の計算を楽に行う
問題1の計算同様、次のように式変形すると楽です。
\begin{eqnarray}
\mathrm{OJ}^2 &=& \left(\frac{60}{11}-4\right)^2+\left(\frac{20}{11}\sqrt{2}-4\sqrt{2}\right)^2\\
&=& \left(\frac{16}{11}\right)^2+\left(\frac{24}{11}\sqrt{2}\right)^2\\
&=& \left(\frac{8}{11}\right)^2\cdot\left(2^2+(3\sqrt{2})^2\right)\\
&=& \left(\frac{8}{11}\right)^2\cdot (4+18)\\
&=& \left(\frac{8}{11}\right)^2\times 22
\end{eqnarray}
解説2. 体積 $V$ の別解
この問題も問題1と同様、立体を半分に割り、底面を別の面に捉えなおします。

\begin{eqnarray}
\triangle\mathrm{ODQ} &=& \frac{1}{2}\triangle\mathrm{ODC}\\
\triangle\mathrm{OPQ} &=& \frac{1}{4}\triangle\mathrm{OBC}
\end{eqnarray}
なので、体積もそれぞれ、$\displaystyle\frac{1}{2}$, $\displaystyle\frac{1}{4}$ であり、求める体積 $V$ は元の体積 $V_{\mathrm{O-ABCD}}$ の
$$\frac{1}{2}\left(\frac{1}{2}+\frac{1}{4}\right)=\frac{3}{8}$$
倍になります。
ここで、元の体積 $V_{\mathrm{O-ABCD}}$ は、
\begin{eqnarray}
V_{\mathrm{O-ABCD}} &=& \frac{1}{3}\cdot\left(\frac{1}{2}\cdot\mathrm{AC}\cdot\mathrm{BD}\right)\cdot\mathrm{OH}\\
&=& \frac{1}{6}\cdot 8\sqrt{2}\cdot 8\sqrt{2}\cdot 4\sqrt{2}\\
&=& \frac{256}{3}\sqrt{2}
\end{eqnarray}
なので、求める体積 $V$ は、
\begin{eqnarray}
V &=& \frac{3}{8}\cdot\frac{256}{3}\sqrt{2}\\
&=& 32\sqrt{2}
\end{eqnarray}
となり、解答に示した値と一致します。
まとめ
正四角錐を底面の辺と隣の辺の中点を結ぶ平面で切断しました。
これも問題1と同じく、高さは、従って全体の体積はすぐに求められます。
また、問題1と同じく、通常は設問の誘導に従って解いていけばよいですが、底面の捉え方を変えることで体積比がすぐに分かることの理解は、今後問題を解いていく際のよい引き出しの一つになると思います。
この場合は全体の体積の $\displaystyle\frac{3}{8}$ になりました。次の式が立体とともに頭に浮かぶようになるとよいです。
$$\frac{3}{8}=\frac{1}{2}\left(\frac{1}{2}+\left(\frac{1}{2}\right)^2\right)$$
この式が頭に浮かべば、今回は中点でしたが、切断ポイントが必ずしも中点でない場合にも応用が利きます。
問題3:四角柱の角を切り落とす
図の立体 $\mathrm{ABCD}-\mathrm{EFGH}$ は、正方形 $\mathrm{ABCD}$ を底面とし、$\mathrm{AB}=4\mathrm{cm}$, $\mathrm{AE}=8\mathrm{cm}$ の直方体である。図のように、辺 $\mathrm{EF}$ 上を動く点 $\mathrm{P}$ は、頂点 $\mathrm{E}$ を出発して、毎秒 $1\mathrm{cm}$ の速さで点 $\mathrm{F}$ に到達するまで動き、辺 $\mathrm{FG}$ 上を動く点 $\mathrm{Q}$ は、頂点 $\mathrm{F}$ を出発して、毎秒 $1\mathrm{cm}$ の速さで点 $\mathrm{G}$ に到達するまで動き、辺 $\mathrm{FB}$ 上を動く点 $\mathrm{R}$ は、頂点 $\mathrm{F}$ を出発して、毎秒 $2\mathrm{cm}$ の速さで点 $\mathrm{B}$ に到達するまで動く。$3$ 点 $\mathrm{P}$, $\mathrm{Q}$, $\mathrm{R}$ が同時に出発するとき、

(1) $\triangle\mathrm{PQR}$ が二等辺三角形になるのは何秒後と何秒後か?
(2) $1$ 秒後のときの四面体 $\mathrm{FPQR}$ の頂点Fから底面 $\mathrm{PQR}$ に下した垂線の長さは何 $\mathrm{cm}$ か?
(20年 東海高校)
$\mathrm{P}$, $\mathrm{Q}$, $\mathrm{R}$ が動いて三角形が変化していくイメージは浮かびますか?この図のイメージです。そして、(1)でいう二等辺三角形は、2か所あります。
(2)は、立体の体積を使って高さを求めます。底面をうまく選ぶことがポイントです。(解説3)
解(1). 二等辺三角形になる時刻
$t$ 秒後は $\mathrm{FP}=4-t$, $\mathrm{FQ}=t$, $\mathrm{FR}=2t$ なので、$\mathrm{PQ}$, $\mathrm{QR}$, $\mathrm{RP}$ の長さは三平方の定理より、
\begin{eqnarray}
\mathrm{PQ}^2 &=& \mathrm{FP}^2+\mathrm{FQ}^2\\
&=& (4-t)^2+t^2\\
&=& 2t^2-8t+16\\
\end{eqnarray}
\begin{eqnarray}
\mathrm{QR}^2 &=& \mathrm{FQ}^2+\mathrm{FR}^2\\
&=& t^2+(2t)^2\\
&=& 5t^2\\
\end{eqnarray}
\begin{eqnarray}
\mathrm{RP}^2 &=& \mathrm{FR}^2+\mathrm{FP}^2\\
&=& (2t)^2+(4-t)^2\\
&=& 5t^2-8t+16
\end{eqnarray}
二等辺三角形になるのは、$\mathrm{PQ}=\mathrm{QR}$, $\mathrm{QR}=\mathrm{RP}$, $\mathrm{RP}=\mathrm{PQ}$ の場合があり得る。
(a) $\mathrm{PQ}=\mathrm{QR}$ の場合
$2t^2-8t+16=5t^2$ より、
\begin{eqnarray}
&&3t^2+8t+16=0\\
&&(3t-4)(t+4)=0\\
&&\therefore\; t=-4,\,\frac{4}{3}
\end{eqnarray}
$t>0$ より、$t=\displaystyle\frac{4}{3}$
(b) $\mathrm{QR}=\mathrm{RP}$ の場合
$5t^2=5t^2-8t+16$ より、
$$t=2$$
(c) $\mathrm{RP}=\mathrm{PQ}$ の場合
$5t^2-8t+16=2t^2-8t+16$ より、
$3t^2=0$。
つまり、$t=0$ となるため、題意に合わない。
従って、
$\displaystyle\frac{4}{3}$ 秒後及び $2$ 秒後。
解(2). 頂点 $\mathrm{F}$ から下した垂線の長さ
$1$ 秒後の図は下図のようになる。

すなわち、$\mathrm{FP}=3$, $\mathrm{FQ}=1$, $\mathrm{FR}=2$ なので、三角錐 $\mathrm{F-PQR}$ の体積 $V$ は、
$$V=1\tag{1}\label{p2867eq1}$$
一方、この体積 $V$ の底面を $\triangle\mathrm{PQR}$ と見立て、その面積を $S$ と置く。
三平方の定理より $\mathrm{PR}=\sqrt{13}$, $\mathrm{RQ}=\sqrt{5}$, $\mathrm{QP}=\sqrt{10}$ なので、$\triangle\mathrm{PQR}$ は下図のようになる。ただし、$\mathrm{Q}$ からPRに下ろした垂線の足を $\mathrm{H}$ と置き、$\mathrm{PH}=x$, $\mathrm{QH}=y$ と置いた。

すると、$\triangle\mathrm{QHP}$, $\triangle\mathrm{QHR}$ は直角三角形であることに注意して三平方の定理を適用すると、
($\rightarrow\;\triangle\mathrm{PQR}$ の高さを求めるアイデアについて:解説1)
\begin{eqnarray}
\left\{ \begin{array}{l}
10=x^2+y^2\\
5=(\sqrt{13}-x)^2+y^2
\end{array}
\right.
\end{eqnarray}
これを解いて、
($\rightarrow$ この連立方程式は意外に簡単:解説2)
\begin{eqnarray}
\left\{ \begin{array}{l}
x=\displaystyle\frac{9}{\sqrt{13}}\\
y=\displaystyle\frac{7}{\sqrt{13}}
\end{array}
\right.
\end{eqnarray}
よって、$\triangle\mathrm{PQR}$ の面積 $S$ は、
\begin{eqnarray}
S &=& \frac{1}{2}\sqrt{13}\frac{7}{\sqrt{13}}\\
&=& \frac{7}{2}
\end{eqnarray}
よって、求める高さ $h$ は\eqref{p2867eq1}を用いて、
\begin{eqnarray}
V &=& \frac{1}{3}Sh\\
&=& \frac{1}{3}\frac{7}{2}h\\
&=&1
\end{eqnarray}
より、
$$h=\frac{6}{7}$$
解説1. $\triangle\mathrm{PQR}$ の高さを求めるアイデアについて
この解法はよく使います。
発想のアイデアとしては、$\triangle\mathrm{PQR}$ の $3$ 辺が分かっているので三角形は一意に決まる、という感覚をまず持つことです。一意に決まる以上、何らかの方法で絶対に求めることができるはず。そしてそれには直角三角形を利用して求める、と。
解説2. この連立方程式は意外に簡単
\begin{eqnarray}
\left\{ \begin{array}{l}
10=x^2+y^2\\
5=(\sqrt{13}-x)^2+y^2
\end{array}
\right.
\end{eqnarray}
という連立方程式を見てギョッとするかもしれないですが、実際解いてみると大したことは無いです。見通しとして、下の式を展開すると $x^2$ と $y^2$ が表れますが、それは上の式にもあるのでこれらはバッサリと消えてくれます。実際、展開すると、
\begin{eqnarray}
\left\{ \begin{array}{l}
10=x^2+y^2\\
5=13-2\sqrt{13}x+x^2+y^2
\end{array}
\right.
\end{eqnarray}
となるため、上の式から下の式を引くことにより、
$$5=-13+2\sqrt{13}x$$
となり、単なる $x$ の一次方程式になります。
解説3. ここの発想がキモ
体積を2通りの見方で捉えることにより高さ $h$ を求めます。この発想は平面図形でも役に立つ場合があります。それが↓の記事です。
まとめ
四角柱の角を切り落としました。
辺の長さや三角形の高さは直角三角形を見つけることにより求めることができます。
そして、平面に下した垂線の長さは、体積を利用して、それも底面の捉え方を変えることで求めることができます。
底面の捉え方を変えると言うことでいえば、平面図形でも同様の発想が使える場面があります。直角三角形の直角頂点から下した垂線の長さ(三角形の高さ)を求める場面です。相似で求めている人が多いと思いますが、この発想を使えばより簡単に出ます。このことは解説3で述べた通りです。
まとめ
立体の切断を扱いました。いずれも難しい問題ですが、考え方としては基礎的で非常にいい問題だと思います。この問題を繰り返し解くことで考え方の基礎がしっかりと身につくと思います。特に、問題1の解説5や問題2の解説2などは平面図形の相似の要素も入っているためにそちらの復習にもなるだけでなく、解答としてもシンプルになります。




コメント