脱力が大事とよく言われます。でも、
力を抜いちゃって、強いボールが打てるの?
などと思ったりしませんか?それを物理的に考えてみます。下記の計算結果は、ラケットはボールに約 50[kg] もの力を与えている、というものです。この力は自分がインパクトの瞬間に与えているものだろうか? と考えると脱力の意味が分かります。
運動量の変化から力の大きさを想像する
力積と運動量変化
一定の力 F が時間 Δt だけ働いたとき、物体には
力積:FΔt
の力積が働き、物体の運動量を変化させます。これを用いてテニスラケットがボールに加える力を想像してみます。
力積については↓の記事で詳しく述べていますのでそちらを確認ください。
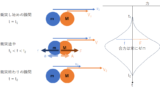
この力積の考え方を利用すると衝突によりどれほどの力が加わっているのかを想像することができます。もちろん正確には力は刻一刻と変わっていてそれを正確に把握することは容易ではありませんが、そこを大雑把に一定の力がかかっているとして考えます。つまり、下図のように青の部分を面積の等しい緑で置き換えて一定の力 ˉf がかかっていると考えます。

このことを利用し、テニスのインパクトではどの程度の力がかかっているかを考えます。問題風にしてみます。
問題風に記載

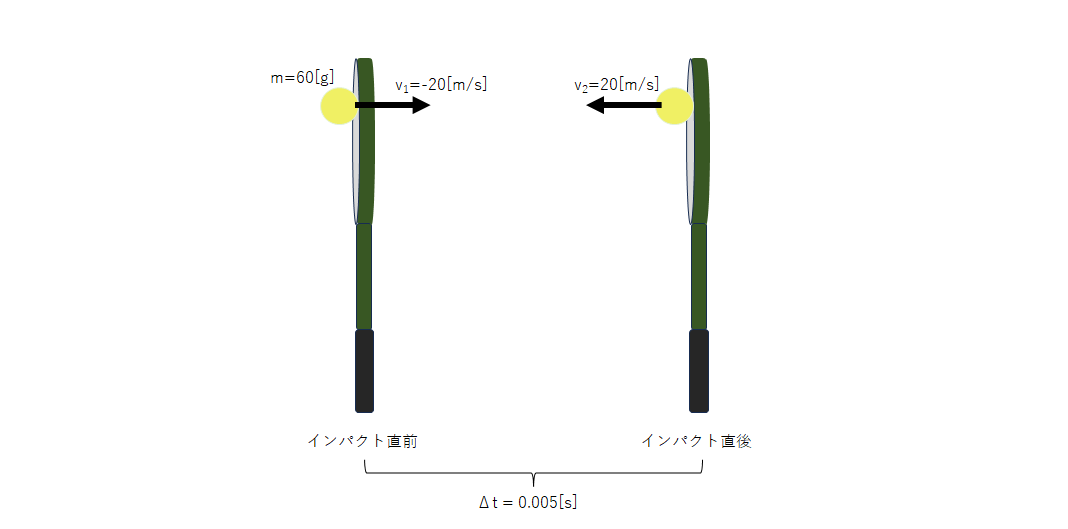
速度 v1=−20[m/s] で飛んできたボールを打ち返したところ、速さは同じで逆の方向を持つ速度 v2=20[m/s] で飛んで行った。このときラケットがボールに加えた力の大きさは平均的にどれほどか。なお、ボールの質量は m=60[g]、インパクト時間は Δt=0.005[s]1とする。
運動量は正負を持つベクトル量なので「速度」という表現で正負を持たせています。力を発する向きを正としたいため、最初の飛来速度が負になっていることに注意してください。
解
ラケットがボールに加えた力を F[N] と置くとラケットがボールに加えた力積は
FΔt
一方、運動量の変化量は
m(v2−v1)
なので、
FΔt=m(v2−v1)
よって、
F=m(v2−v1)Δt=0.06×{20−(−20)}0.005=480[N]≃49[kgf]
となります。約 50[kg] の力が加わっていることがわかります。
まとめ:脱力の意味
インパクトの瞬間を超スローで見たことのある人はボールが半分くらいつぶれている映像を知っていると思いますが、確かにこれくらいの力が加わっていそうですよね。この計算で改めて思うことは、人はこんな力を出せない、ということです。つまり、ボールを強く打とうとインパクトの瞬間にボールに力を加えることはナンセンス、ということです。ボールはこれまでに加速して速度を持ったラケットとの衝突運動で飛んでいくのであって、インパクトの瞬間に人が加えている力で飛んで行っているわけではありません。インパクトの瞬間に力をこめるのではなく、それまでにいかにヘッドスピードを上げられるか、が強いボールを打つためのカギだということがこの計算から考察できます。
今回は運動量と力積の関係から脱力の意味を考察しました。↓の記事では脱力に勝るとも劣らないほど重要な、運動連鎖の理論について考察しています。
また↓の記事では運動量保存の法則を用いることでラケットの最適な重さを考えています。
そして↓の記事では等加速度運動の公式からテニスを考察しています。
- 例えば、テニス指導教本 財団法人日本テニス協会編 大修館書店 p23 表3-1、 テクニカルテニス Rod Cross, Crawford Lindsey; 常盤 泰輔訳, p16 ↩︎



コメント