【運動量保存の法則】運動方程式でも解いてみる　実は同じこと、と分かると気が楽に！！

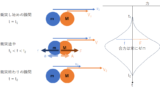
　運動量保存の法則と運動方程式と両方で解いて、両方が同じ結果になることを確かめます。そして、なぜ同じになるのかを考察します。問題のイメージは↓この図です。このシミュレーションの諸元はシミュレーションの諸元に示しています。

ここの「解説」にてなぜ同じになるのかを考察していますが、加えて↓の記事を読むことでさらに完全理解しましょう。それが理解できれば、どちらが楽に解けるのかで選べばよいという余裕が生まれます。

問題設定

　状況はイメージできるでしょうか。下の台車だけ $t=0$ に、例えばハンマーなどでガツンとたたかれて速度を急に持ったような状況です。そして、台車と物体の間には摩擦があるので物体は台車に引きずられて動いていくが、少し滑っていずれ台車と同じ速度で、つまり台車上に止まった状態で一体となって動いていく、というものです。

解1. 運動量保存の法則で解く

運動量保存の法則より、

$$Mv_0 + m\cdot 0 = (M+m)v_1$$

よって、

$$v_1=\frac{M}{M+m}\, v_0$$

解2. 運動方程式で解く

物体が台車上で滑っている状態を考える。このときに加わる力は下図のようである。

物体mの運動方程式：

$$\begin{eqnarray} \left\{ \begin{array}{l} ma =\mu N_1\\ 0 = N_1 – mg\tag{1}\label{p1232eq1} \end{array} \right. \end{eqnarray}$$

台車Mの運動方程式：

$$MA=-\mu N_1\tag{2}\label{p1232eq2}$$

式$\eqref{p1232eq1}$より

$$a=\frac{\mu N_1}{m}=\frac{\mu mg}{m}=\mu g$$

物体mはこの加速度で加速して初速度 $0$ から速度 $v_m$ を持つようになるので、$t$ 秒後の速度 $v_m$ は、

$$v_m = at = \mu g t\tag{3}\label{p1232eq3}$$

また、式$\eqref{p1232eq2}$より

$$A=-\frac{\mu N_1}{M}=-\frac{\mu mg}{M}$$

物体Mはこの加速度で加速して初速度 $v_0$ から速度 $v_M$ を持つようになるので、$t$ 秒後の速度 $v_M$ は、

$$v_M = v_0+At = v_0-\frac{\mu mg}{M}\, t\tag{4}\label{p1232eq4}$$

$v_M=v_m\, (=v_1)$ になると摩擦力は働かなくなりそれ以降は同じ速度で動く。この時刻を $t_1$ とすると式$\eqref{p1232eq3}$, $\eqref{p1232eq4}$より、

$$\begin{eqnarray} \begin{array}{c} \mu gt_1=v_0-\displaystyle\frac{\mu mg}{M}\, t_1\\ \therefore\;t_1=\displaystyle\frac{M}{\mu (M+m)g}\, v_0 \end{array} \end{eqnarray}$$

このときの速度 $v_1$ は式$\eqref{p1232eq3}$を使うと、

$$\begin{eqnarray} v_1&=&\cancel{\mu}\cancel{g}\frac{M}{\cancel{\mu}(M+m)\cancel{g}}\, v_0\\ &=&\frac{M}{M+m}\, v_0 \end{eqnarray}$$

解1と同じ結果を得た。

解説. 運動量保存の法則も結局は運動方程式を解いている

　ここでは解1と解2の関係がより分かるよう、また↓の記事との比較がしやすいように解説をします。

解1の復習：運動量保存の法則の導出をなぞる

解2で立てた運動方程式から解1を導きます。横方向の運動方程式のみを示します。

$$\begin{eqnarray} \left\{ \begin{array}{l} ma &=& \mu N_1\\ MA &=& -\mu N_1 \end{array} \right. \end{eqnarray}$$

上下の式の和を取ると、

$$ma+MA = 0\tag{5}\label{p1232eq5}$$

です。これを $t=0$ から $t=t_1$ まで積分すると、

$$\begin{eqnarray} \begin{array}{c} \displaystyle m\int_0^{t_1}a\, dt + M\int_0^{t_1}A\, dt = 0\\ \displaystyle m\int_0^{t_1}\frac{dv}{dt}\, dt + M\int_0^{t_1}\frac{dV}{dt}\, dt = 0\\ \displaystyle m\int_0^{v_1}dv + M\int_{v_0}^{v_1}dV = 0\\ m(v_1-0) + M(v_1-v_0) = 0 \end{array} \end{eqnarray}$$

となり、解1で解いた運動量保存の法則が導かれます。この式変形は運動量保存の法則の導出をなぞったもので↓の記事の内容ですが、ここではこれを丁寧に解2と結びつけます。

解2と解1を結び付ける

$$m\int_0^{t}a\, dt + M\int_0^{t}A\, dt = 0\tag{6}\label{p1232eq6}$$

を少し深堀りします。$\int$ 記号の上側を $t(>0)$ にしていることに注意してください。$t>0$ ならどの時刻においても運動方程式の上下の和は$\eqref{p1232eq5}$なので$\eqref{p1232eq6}$は成り立ちます。

ここで、第1項と第2項の積分の値は$\eqref{p1232eq3}$と$\eqref{p1232eq4}$の記号を用いると、

$$\begin{eqnarray} \int_0^t a\,dt &=& v_m-0\\ \int_0^t A\,dt &=& v_M-v_0 \end{eqnarray}$$

と書け、$\eqref{p1232eq6}$は、

$$m(v_m-0) + M(v_M-v_0) = 0\tag{7}\label{p1232eq7}$$

となります。この式は確かに冒頭のシミュレーションの絵からも納得できます。下図に具体的な時刻 $t=0.5,\, 1,\, 2$ でそれを示します。

例えば $t=0.5$ では物体Mの速度は初速度 $5$ から $4.4$ になり $-0.6$ だけ変化しています $(v_M-v_0=4.4-5=-0.6)$、一方物体mの速度は初速度 $0$ から $1$ 変化しています$(v_m-0=1)$。そして、それぞれの速度に質量$(M=10,\, m=6)$を掛けた数字が真ん中に記載されており、それらは $-6$ と $6$ です。両者の和は $0$ になっており、確かに$\eqref{p1232eq7}$の

$$\begin{eqnarray} \begin{array}{c} m(v_m-0) + M(v_M-v_0) = 0\tag{7再掲}\\ 6(1-0)+10(4.4-5)=0 \end{array} \end{eqnarray}$$

が成り立っています。他の時刻でも同様の関係にあり、常に$\eqref{p1232eq7}$の関係が成り立っています。

外力が働かない限り常にこの式が成り立っているわけで、それが運動量保存の法則が主張していることです。そして、例えば $t=2$ ではすでに $v_m$ と $v_M$ は一緒の速度になっており、このときにも$\eqref{p1232eq7}$は成り立っているので、$v_m=v_M=v_1$ と置いて、

$$m(v_1-0) + M(v_1-v_0) = 0$$

から $v_1$ を求めるのが運動量保存の法則で解くやり方というわけです。

この式は $v_m$ と $v_M$ の関係を知るには非常に便利ですが、一方で各時刻での速度は分かりません。時刻 $t$ での速度を求めようと思えば、解2で行ったように$\eqref{p1232eq1}$, $\eqref{p1232eq2}$から加速度を求めて時間で積分します。

でも今は加速度を求める必要も、各時刻における速度を求める必要もないため、$\eqref{p1232eq1}$, $\eqref{p1232eq2}$の両者を足して余分な $\mu N_1$ といった項を消した状態で積分した「運動量保存の法則」の方が便利に解ける、ということです。

まとめ：解1も解2も結局は運動方程式を解いている

　以上のように、$\eqref{p1232eq1}$, $\eqref{p1232eq2}$から加速度を求め、そこから速度を求めるといった解2の方法でも、また$\eqref{p1232eq1}$, $\eqref{p1232eq2}$を足して外力がゼロという性質を使って余分な項を消した状態から速度を求める解1の方法でも、結局はどちらも運動方程式を解いていることは同じです。

表題には「運動方程式でも解いてみる」と銘打っていますが、結局は運動量保存の法則も運動方程式を解いているということを理解できれば、本質は同じであり単に解きやすい方法で解いているに過ぎない、と理解ができ、気が楽になります。こちらの記事↓も見て完全理解を目指してください。

シミュレーションの諸元

　冒頭に示したシミュレーションの諸元は次の通りです。

• $M=10$ [kg]
• $m=6$ [kg]
• $\mu=0.2$
• $v_0=5$ [m/s]
• $g=9.8$ [m/s$^2$]

この時の最終的な速度 $v_1$ は、

$$v_1 = \frac{M}{M+m}\, v_0 = \frac{10}{10+6}\times 5 = 3.125\;\mathrm{[m/s]}$$

$t_1$ は、

$$t_1 = \frac{M}{\mu (M+m)g}\, v_0 = \frac{10}{0.2\times (10+6)\times 9.8}\times 5 = 1.594\;\mathrm{[s]}$$

また、シミュレーションではもう一つ、

• $dt=0.01$ [s]

を設定しています。冒頭の動画で最終速度が $3.125$ になっていないのはこの $dt$ の間隔が十分には小さくないからです。この $dt$ を $0.00001$ にしたら、少なくとも有効数字3桁では $3.125$ になりました。

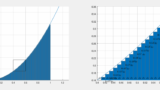
この $dt$ の例からも分かるように、積分は細かい短冊の寄せ集めです。$dt=0.01$ でもほぼほぼ正しい値にはなりますが少しずれます。$dt=0.00001$ にすればもっと正しい値になります。そして積分記号としての $dt$ は無限に小さい足し合わせのため、正確です。

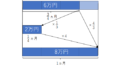
積分は細かい短冊の寄せ集めであるイメージは↓の記事で述べています。円の面積 $\pi r^2$ と円周の長さ $2\pi r$ が微分積分の関係であることがすっきりと分かります！