場合の数を数えるのは何かとミスしがちですが、基本的なところは慣れでカバーができます。今回はそのような代表例、基本例を流し読みできるような形で記載しましたので、何回も見て慣れましょう。
さいころ系：2回投げる
1回目と2回目がそれぞれ独立して試行されるケースです。具体的にはさいころが良い例で、1回目に出る目は6通りあり、2回目に出る目は1回目の結果に左右されず（このことを「独立事象」という）6通りあるので、2回さいころを投げたときの目の出かたは全部で、
$$6\times 6=36$$
通りあります。なお、「同時に投げる」と表現しても全く同じです。一方のさいころの出方は他方には影響されず、独立事象であることに変わりはないからです。あるいは感覚的には、いくら同時に投げたとしても、厳密には若干の時間差があるので1回目と2回目が定義される、との理解もできます。
以降、さいころを2回投げる（あるいは2個のさいころを同時に投げる）場合の問題例として考えていきます。そうすると分母は全て $6\times 6=36$ 通りなので、分子の場合の数を考えることが課題になります。
目の数の和が7
題意のようになる場合は、
$$(1,6),\; (2,5),\; (3,4),\; (4,3),\; (5,2),\; (6,1)$$
の $6$ 通りあるから、求める確率は、
$$\frac{6}{36}=\frac{1}{6}$$
目の数の和が8
題意のようになる場合は、
$$(2,6),\; (3,5),\; (4,4),\; (5,3),\; (6,2)$$
の $5$ 通りあるから、求める確率は、
$$\frac{5}{36}$$
目の数の和が3の倍数
題意のようになる場合は、
$$(1,2),\; (1,5),\; (2,1),\; (2,4),\; (3,3),\; (3,6),\; (4,2),\; (4,5),\; (5,1),\; (5,4),\; (6,3),\; (6,6)$$
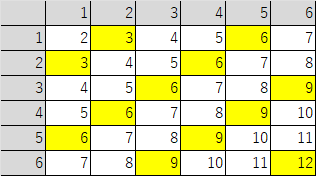
の $12$ 通りあるから、求める確率は、
$$\frac{12}{36}=\frac{1}{3}$$
1回目の目を十の位、2回目の目を一の位としてできる数字が3の倍数
題意のようになる場合は、
$$(1,2),\; (1,5),\; (2,1),\; (2,4),\; (3,3),\; (3,6),\; (4,2),\; (4,5),\; (5,1),\; (5,4),\; (6,3),\; (6,6)$$
すなわち、$12$ 通りあるから、求める確率は、
$$\frac{12}{36}=\frac{1}{3}$$
目の数の和が3の倍数の問題と同じ
ある数が $3$ の倍数であるかどうかを見分ける裏技として次があります。
ある数字が $3$ の倍数 $\iff$ その数字の各位の和が $3$ の倍数
例えば $21$ は、$2+1=3$ で $3$ の倍数なので、$21$ は $3$ の倍数である、と判別できるというわけです。そう考えると、先ほどの問題「目の数の和が3の倍数」と同じ結果になることが理解できます。
少なくとも1回は奇数の目
題意のようになる場合は下図の黄色の部分。
すなわち、$27$ 通りあるから、求める確率は、
$$\frac{27}{36}=\frac{3}{4}$$
少なくとも系は、逆側の事象を考えると楽な場合が多い
上記はまともに数えましたが、よくよく考えれば題意は、
「両方ともが偶数」ではない場合
です。両方ともが偶数の場合の数は上図の白抜き部分なので $9$ 通りです。このことを使って解答してもよく、その場合は次のような感じになります。
別解1
「両方ともが偶数」の場合は $9$ 通りあるので、「少なくとも1回が奇数」は $36-9=27$ 通り。従って求める確率は、
$$\frac{27}{36}=\frac{3}{4}$$
別解2
「両方ともが偶数」の場合は $9$ 通りあり、その確率は、
$$\frac{9}{36}=\frac{1}{4}$$
「少なくとも1回が奇数」は「両方ともが偶数」が起こらなかった場合なので、求める確率は、
$$1-\frac{1}{4}=\frac{3}{4}$$
順列系
ここではすでに↓の記事を読んだものとして、楽に数えます。
A,B,C,D,E の並べ方
$$5!=5\times 4\times 3\times 2\times 1=120$$
通り。
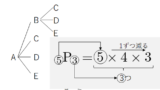
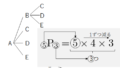
A,B,C,D,E から3つを選び並べるときの並べ方
$$_5\mathrm{P}_3=5\times 4\times 3=60$$
通り。
1～6のカードを2枚取り出し、1枚目を十の位、2枚目を一の位で3の倍数
さいころ系の問題と類似ですが、さいころ系は独立事象で $6\times 6$ 通りでしたが、こちらは順列です（1枚目に取ったカードは2枚目には出てこない）。
場合の数は
$$_6\mathrm{P}_2 = 6\times 5 = 30$$
通り。このうち、3の倍数になるのは1枚目と2枚目の数字の和が3になるケースであり、次の10通り。
$$(1,2),\; (1,5),\; (2,1),\; (2,4),\; (3,6),\; (4,2),\; (4,5),\; (5,1),\; (5,4),\; (6,3)$$
よって求める確率は
$$\frac{10}{30}=\frac{1}{3}$$
組み合わせ系
ここも同様に、↓の記事を読んだものとして、楽に数えます。
5人から2人を選ぶ選び方
選ばれた2人には順番は不要なので、組み合わせで数えることになります。すなわち、
\begin{eqnarray}
_5\mathrm{C}_2 &=& \frac{5\times 4}{2\times 1}\\
&=& \frac{5\times \cancel{4}^2}{\cancel{2}\times 1}\\
&=& 10
\end{eqnarray}
5人から2人選ぶとき、自分が選ばれる確率（5人のうちの一人が自分）
5人をA,B,C,D,Eと書き、自分をAとしても一般性を失わない。5人から2人を選ぶ選び方は上で求めており、
$$_5\mathrm{C}_2 = \frac{5\times \cancel{4}^2}{\cancel{2}\times 1} = 10$$
通り。
一方、自分が選ばれるのは、(A,B), (A,C), (A,D), (A,E) の4通り。よって、自分が選ばれる確率は、
$$\frac{4}{10}=\frac{2}{5}$$
青玉4個、白玉2個から2個を取り出す
同じものが複数ある場合です。このときは、同じものでも一旦別々のものとして数えます。
確率は、同じものでも区別する
まず、2個を取り出すと言っているので、その場合の数を数えておきます。これが分母になります。青玉4個と白玉2個の計6個（別々のものとして考える）から2個を取り出す場合の数なので、
\begin{eqnarray}
_6\mathrm{C}_2 &=& \frac{6\times 5}{2\times 1}\\
&=& \frac{\cancel{6}^3\times 5}{\cancel{2}\times 1}\\
&=& 15
\end{eqnarray}
通り。
2個とも青玉の確率
青玉は4個あり、この4個から2個が選ばれる場合の数を数えればよいから、
\begin{eqnarray}
_4\mathrm{C}_2 &=& \frac{4\times 3}{2\times 1}\\
&=& \frac{\cancel{4}^2\times 3}{\cancel{2}\times 1}\\
&=& 6
\end{eqnarray}
よって求める確率は、
$$\frac{6}{15}=\frac{2}{5}$$
2個とも白玉の確率
白玉は2個あり、この2個ともが選ばれる場合なので1通り。
よって求める確率は、
$$\frac{1}{15}$$
青玉と白玉が1個ずつの確率
青玉は4つあり、白玉は2つある。それぞれから1つずつ選ぶ選び方は
$$4\times 2=8$$
通り。実際、樹形図を書くと下記のようになり、確かに8通り。
よって求める確率は
$$\frac{8}{15}$$
全ての確率を足すと確かに1になっている
2個を取る場合はこれ以外に取り方は無いので、上記の確率を足すと確かに
$$\frac{6}{15}+\frac{1}{15}+\frac{8}{15}=1$$
となっています。
まとめ
確率の問題の代表例をザーッと眺めてきました。場合の数を数えるのは何かとミスしがちですが、基本的なところは慣れでカバーができます。今回はそのような代表例、基本例を流し読みできるような形で記載しましたので、何回も見て慣れましょう。
コメント