場合の数の数え方の基本は樹形図を描くことです。これは必ずマスターしましょう。その上で「順列」「組み合わせ」の概念を知ることにより、そしてそれに記号を導入することにより、かなり見通しが良くなります。記号の導入は高校範囲ですが、中学生でも理解できる内容です。
樹形図を書く基本形（中学内容）
A,B,C の順列
順列とは、並べ方のことです。樹形図を描くと下記の6通りあることが分かりますが、これをネタに深堀していきます。
すなわち、先頭には A か B か C の3通りの並べ方があり、2番目にはそれぞれに対して2通りの並べ方があり、そして最後はそれぞれに対して1通りの並べ方があります。従ってその総数は、
$$3\times 2\times 1=6$$
と計算できることになります。
A,B,C,D,E の順列
考え方は先ほどと同じですが、樹形図を描くのは大変になってきます。少しさぼって描きます。
この場合も先ほどと同じように、先頭には5通りの並べ方があり、2番目にはそれぞれに対して4通りの並べ方があり、$\cdots$ となり、従ってその総数は、
$$5\times 4\times 3\times 2\times 1=120$$
と計算できます。
A,B,C,D,E から3つを選んだ順列
今度は一部だけを使う例となります。樹形図は同様ですが、途中までです。先ほどの樹形図のうち、3つ目までを持ってくればよいですね。
従ってその総数は、
$$5\times 4\times 3=60$$
と計算できます。
A,B,C,D,E から3つを選んだ組み合わせ
先ほどとの違いは、「順列」が「組み合わせ」になっている点です。組み合わせとは、順番を気にしない選び方です。例えば、(A,B,C)の組み合わせを選ぶ場合、↓の6通りの並べ方（再掲）は全て同じ組み合わせと見なします。
とすれば、先ほどの順番を気にする並べ方（順列）では
$$5\times 4\times 3=60$$
と計算したものに対し、それぞれ6通りずつ同じ組み合わせが生じることになるので、組み合わせの数としては、
$$60\div 6=10$$
となります。
記号を導入してすっきりさせる（高校内容）
先ほどと同じ例を記号を使ってすっきりとさせます。この記号は高校で出てくるので、中学生は知らなくても構わないのですが、知っているとすっきりと見通しがよくなり、有利です。
A,B,C の順列
下図（再掲）より
$$3\times 2\times 1=6$$
通りですが、このように、一つずつ数字が減り1まで掛けていくとき、
$n!$ と書き、「$n$ の階乗」と読む。
すなわち、
$n$ 個のもの全てを並べる順列は $n!$ 通り
です。
A,B,C,D,E の順列
$5$ 個のもの全てを並べる順列なので、
$$5!=5\times 4\times 3\times 2\times 1=120$$
通り。
A,B,C,D,E から3つを選んだ順列
下図（再掲）より
$$5\times 4\times 3=60$$
通りですが、これを
$_5\mathrm{P}_3$ と書き、「$5$ ピー $3$」と読む。
$\mathrm{P}$ は Permutation の頭文字で、順列を意味する英語です。
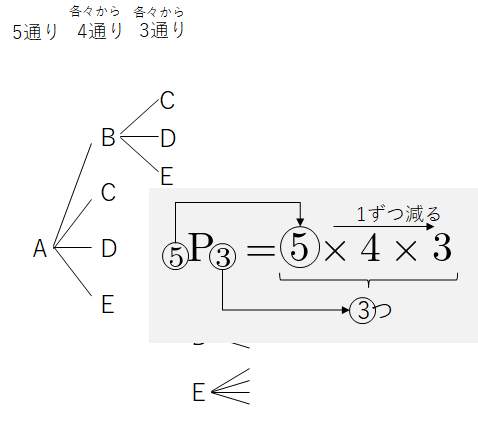
ここで、$5$ や $3$ の添え字と実際の計算式との関係をより明確にしておきます。下図です。
A,B,C,D,E から3つを選んだ組み合わせ
組み合わせは、一旦順列を考えた上で、同じ組み合わせになる下図（(A,B,C)の例：再掲。6通り）で割ればよいです。
従ってこの場合は、まずは、A,B,C,D,E の5つから3つを選ぶ順列は
$$_5\mathrm{P}_3=5\times 4\times 3=60$$
通りで、選んだ3つはそれぞれ
$$3!=3\times 2\times 1=6$$
通りずつが同じ組み合わせなので、結局組み合わせとしては
$$60\div 6=10$$
通りです。これを
$_5\mathrm{C}_3$ と書き、「$5$ シー $3$」と読む。
$\mathrm{C}$ は Combination の頭文字で、組み合わせを意味する英語です。
ここで、$5$ や $3$ の添え字と実際の計算式との関係をより明確にしておきます。下図です。
まとめ
順列と組み合わせについて見てきました。順列は順番を気にする数え方で、組み合わせは順番を気にしない数え方です。そしてそれぞれを記号で表しました。すなわち、
$n$ 個の中から $r$ 個を選ぶ順列は、
$n$ 個の中から $r$ 個を選ぶ組み合わせは、
です。
このように記号で表すことにより立式の意味がつかみやすくなり、またその後は単なる計算に落とし込めるため、見通しがよくなります。
コメント