【平面のベクトル方程式】それは空間上に浮かぶ座標平面　媒介変数(パラメータ)の意味もアニメーションでよくわかる

　平面は3点が与えられれば決まります。あるいは同じことですが、1点と2つのベクトルが与えられれば決まります。このことをイメージで理解し、ベクトル方程式という形で楽に書きます。

　ベクトル方程式が書ければ軌跡方程式への変換は法線ベクトルと内積を取るだけで済むので、ベクトル方程式を楽に書けることがまずは重要です。

　平面のベクトル方程式を理解するには一次独立や内積について知っておく必要があります。↓の記事で詳しく扱っています。

　難関大学ではここで述べる考え方をふんだんに付加う問題がよく出ます。例えば↓の記事にて紹介しています。

平面のベクトル方程式

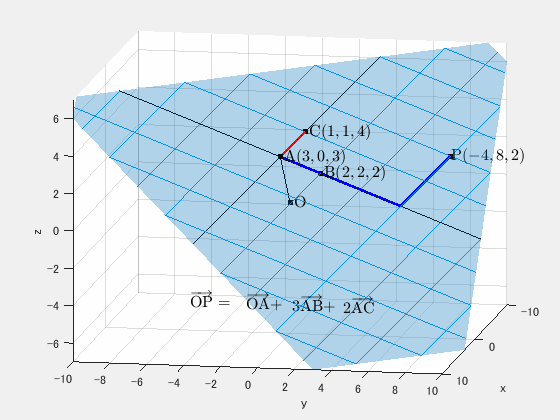
平面は2つのベクトルで張られる：$\overrightarrow{\mathrm{OP}} = \overrightarrow{\mathrm{OA}} + s\,\overrightarrow{\mathrm{AB}} + t\,\overrightarrow{\mathrm{AC}}$

　平面は2つの一次独立なベクトルで形成されます。空間上に浮かぶ平面の場合は媒介変数(パラメータ) $s,\, t$ を用いて次のように表せます。

これは、

点 $\mathrm{A}$ を通り、ベクトル $\overrightarrow{\mathrm{AB}}$, $\overrightarrow{\mathrm{AC}}$ で張られる平面

と表現されます。そのことを下記↓のアニメーションでイメージします。

確かに点 $\mathrm{A}$ やベクトル $\overrightarrow{\mathrm{AB}}$, $\overrightarrow{\mathrm{AC}}$ の存在は確認できました。しかしまだモヤモヤが残っていますか？それは、$s$ や $t$ は何を表すのか？といったところでしょうか。

$s$, $t$ は媒介変数(パラメータ)といい、新しい座標軸平面での座標を表す

　上のアニメーションで最後に碁盤の目が表れてきました。$s$ や $t$ は媒介変数またはパラメータと呼びますが、この平面上（平面 $\alpha$ と呼ぶことにします）の点 $\mathrm{P}$ が碁盤の目のどこに位置するかを表します。

例えば点 $(-4,8,2)$ は平面 $\alpha$ 上の点ですが、この点の場合は $s=3$, $t=2$ で表現できます。まずは計算で求めましょう。$\overrightarrow{\mathrm{AB}}=(-1,2,-1)$, $\overrightarrow{\mathrm{AC}}=(-2,1,1)$ であることから、

$$\begin{eqnarray} \overrightarrow{\mathrm{OP}} &=& \overrightarrow{\mathrm{OA}} + 3\overrightarrow{\mathrm{AB}} + 2\overrightarrow{\mathrm{AC}}\\ &=& \begin{pmatrix}3\\0\\3\end{pmatrix} + 3\begin{pmatrix}-1\\2\\-1\end{pmatrix} + 2\begin{pmatrix}-2\\1\\1\end{pmatrix}\\ &=& \begin{pmatrix}-4\\8\\2\end{pmatrix} \end{eqnarray}$$

と計算でき、確かに点 $(-4,8,2)$ となります。

同様に点 $(7,1,-2)$ は $s=2$, $t=-3$ で、

$$\begin{eqnarray} \overrightarrow{\mathrm{OP}} &=& \overrightarrow{\mathrm{OA}} + 2\overrightarrow{\mathrm{AB}} – 3\overrightarrow{\mathrm{AC}}\\ &=& \begin{pmatrix}3\\0\\3\end{pmatrix} + 2\begin{pmatrix}-1\\2\\-1\end{pmatrix} – 3\begin{pmatrix}-2\\1\\1\end{pmatrix}\\ &=& \begin{pmatrix}7\\1\\-2\end{pmatrix} \end{eqnarray}$$

と計算できます。

以上をアニメーションで再確認します。

この新しい座標軸上の任意の点は $s$, $t$ を適切に定めることにより表現できることは、この碁盤の目を想像すると理解できますね。

$\overrightarrow{\mathrm{OP}} = (1-s-t)\,\overrightarrow{\mathrm{OA}}+s\,\overrightarrow{\mathrm{OB}}+t\,\overrightarrow{\mathrm{OC}}$ とも表現できる

　以下の２式はどちらも同じ平面を表します。

$$\overrightarrow{\mathrm{OP}} = \overrightarrow{\mathrm{OA}} + s\,\overrightarrow{\mathrm{AB}} + t\,\overrightarrow{\mathrm{AC}}\tag{1}\label{p5466eq1}$$

$$\overrightarrow{\mathrm{OP}} = (1-s-t)\,\overrightarrow{\mathrm{OA}}+s\,\overrightarrow{\mathrm{OB}}+t\,\overrightarrow{\mathrm{OC}}\tag{2}\label{p5466eq2}$$

ここでは、式$\eqref{p5466eq2}$を変形して式$\eqref{p5466eq1}$になることを示します。

$$\begin{eqnarray} \overrightarrow{\mathrm{OP}} &=& (1-s-t)\,\overrightarrow{\mathrm{OA}}+s\,\overrightarrow{\mathrm{OB}}+t\,\overrightarrow{\mathrm{OC}}\\ &=& \overrightarrow{\mathrm{OA}} + s\,(\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}) + t\,(\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OA}})\\ &=& \overrightarrow{\mathrm{OA}} + s\,\overrightarrow{\mathrm{AB}} + t\,\overrightarrow{\mathrm{AC}} \end{eqnarray}$$

平面の軌跡方程式

$ax+by+cz=d$ の式にするには？ 法線ベクトルと内積を取ると・・・

　もう一つの平面の式の形に

$$ax+by+cz=d$$

の形があります。ベクトル方程式からこの軌跡の式に変形するのは「外積」の考え方を使えば簡単です。

「外積」の考え方を使えば、ベクトル $\overrightarrow{\mathrm{AB}}=(-1,2,-1)$ とベクトル $\overrightarrow{\mathrm{AC}}=(-2,1,1)$ の双方に垂直なベクトルの一つ $\overrightarrow{n}$ は

$$\overrightarrow{n} = \begin{pmatrix}1\\1\\1\end{pmatrix}$$

です。実際に内積を取ってみると確かにゼロになることがすぐに確かめられます。

そして、この $\overrightarrow{n}$ とベクトル方程式とで内積を取ることで軌跡の式が得られます。

$$\begin{eqnarray} \overrightarrow{n}\cdot\overrightarrow{\mathrm{OP}} &=& \overrightarrow{n}\cdot\overrightarrow{\mathrm{OA}} + s\;\overrightarrow{n}\cdot\overrightarrow{\mathrm{AB}} + t\;\overrightarrow{n}\cdot\overrightarrow{\mathrm{AC}}\\ \begin{pmatrix}1\\1\\1\end{pmatrix}\cdot\begin{pmatrix}x\\y\\z\end{pmatrix} &=& \begin{pmatrix}1\\1\\1\end{pmatrix}\cdot\begin{pmatrix}3\\0\\3\end{pmatrix} + s\;\begin{pmatrix}1\\1\\1\end{pmatrix}\cdot\begin{pmatrix}-1\\2\\-1\end{pmatrix} + t\;\begin{pmatrix}1\\1\\1\end{pmatrix}\cdot\begin{pmatrix}-2\\1\\1\end{pmatrix} \end{eqnarray}$$

$$\therefore\; x+y+z=6$$

となります。見事に $s$, $t$ の係数部分が消えるわけです。

このように見ると、軌跡の式の $x$, $y$, $z$ の係数を並べたベクトル（この場合は $(1,1,1)$）が法線ベクトルになることがよくわかりますね。

まとめ

　平面のベクトル方程式と軌跡方程式を見てきました。平面は3点が与えられれば決まりますが、それを1点と2つの一次独立のベクトルに見立てると平面のベクトル方程式が得られ、そこに法線ベクトルと内積を取ると軌跡の方程式が得られます。

法線ベクトルは外積によって求められます。↓の記事で述べています。