#5394にリンク元
ベクトルという道具を使いこなすメリットは、図形の問題をあまり特殊な発想を持たなくても解けることです。いやいや、ベクトルは難しいよ、という人は道具の使い方に慣れていないためだと思います。ここではその道具の全体像を示すことで、どのような問題にどの道具を使えばよいのかが整理できます。
直線上の点問題(兼 平行問題)

\overrightarrow{\mathrm{OP}} = t\,\overrightarrow{\mathrm{OA}} + (1-t)\,\overrightarrow{\mathrm{OB}}
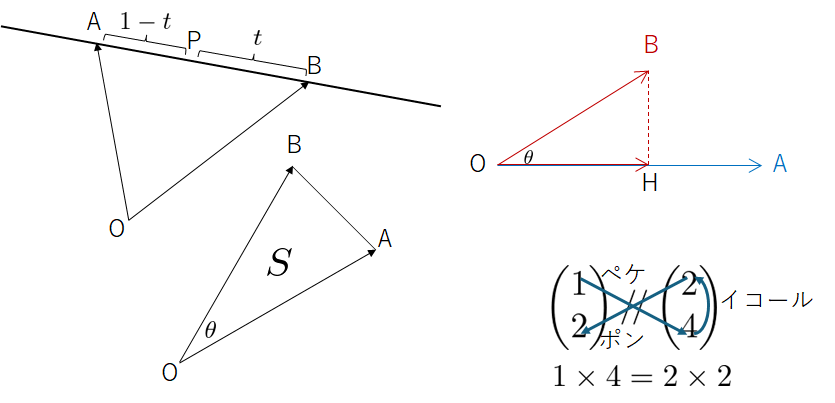
点 \mathrm{P} が点 \mathrm{A} と \mathrm{B} を通る直線上にある場合、
\overrightarrow{\mathrm{OP}} = t\,\overrightarrow{\mathrm{OA}} + (1-t)\,\overrightarrow{\mathrm{OB}}\tag{1}\label{p5394eq1}
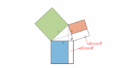
と表せますが、これを下記の図で説明します。

この図の左は通常私たちが目にする座標平面ですが、点 \mathrm{A} と点 \mathrm{B} を通る直線といえば、
x+y=1
ですよね。これは、まずは x, y に制限を設けなければ平面上の任意の点 \mathrm{P} が
\overrightarrow{\mathrm{OP}} = x\,\overrightarrow{\mathrm{OA}} + y\,\overrightarrow{\mathrm{OB}}
で表され、さらに点 \mathrm{A} と点 \mathrm{B} を通る直線という制限下では
x+y=1
ということですから確かに式\eqref{p5394eq1}となっています。
そしてこの \overrightarrow{\mathrm{OA}} と \overrightarrow{\mathrm{OB}} は先の図の右のように斜めになっていても全く同じなので、任意の \overrightarrow{\mathrm{OA}} と \overrightarrow{\mathrm{OB}} に対して式\eqref{p5394eq1}は成り立ちます。
どちらが t でどちらが 1-t だったか問題:私の場合
式\eqref{p5394eq1}の形は分かったけれども、
点 \mathrm{P} は点 \mathrm{A}, \mathrm{B} を
- t:1-t に内分するのか
- 1-t:t に内分するのか
ちょっとわからなくなりませんか?教科書によっては「たすき掛けで覚えよ」とか書いてあるものもありますが、私の理解の仕方を参考に述べます。
私の場合は具体的な数字を入れて実験します。具体的な数字とは、t=0 と t=1 です。
t=0 を入れてみると式\eqref{p5394eq1}は
\begin{eqnarray} \overrightarrow{\mathrm{OP}} &=& 0\,\overrightarrow{\mathrm{OA}} + (1-0)\,\overrightarrow{\mathrm{OB}}\\ &=& \overrightarrow{\mathrm{OB}} \end{eqnarray}
となるので、↓の図の右側が正しいことが分かります。

\overrightarrow{\mathrm{AP}} = k\overrightarrow{\mathrm{AB}}
もう一つの直線上の表し方です。始点がそろっている場合はこれを用いるのが楽です。
例えば次のような例題を考えてみます。
点 \mathrm{P} が直線 \mathrm{AB} 上にあるとき \mathrm{P} の座標を求めよ。

図の点 \mathrm{P} は直線 \mathrm{AB} にはないですが、直線 \mathrm{AB} にあれば
\overrightarrow{\mathrm{AP}} = k\,\overrightarrow{\mathrm{AB}}
が成り立ちます。よって、
\begin{pmatrix}p-1\\p\end{pmatrix} = k\begin{pmatrix}2\\4\end{pmatrix}
から k, p を求めれば、
k=\displaystyle\frac{1}{2},\; p=2
\therefore\mathrm{P}(2,3)
と求まります。
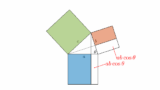
\overrightarrow{\mathrm{AP}} /\! / \overrightarrow{\mathrm{AB}} は、ペケ・イコール・ポン
しかし、わざわざ k を持ち出さなくても p は求められます。平行のベクトルでは、ペケ・イコール・ポンが成り立ちます。例えば、
\begin{pmatrix}1\\2\end{pmatrix} /\! / \begin{pmatrix}2\\4\end{pmatrix}
の場合、

といった具合です。これを用いて先の問題を考えると、
\begin{pmatrix}p-1\\p\end{pmatrix} /\! / \begin{pmatrix}1\\2\end{pmatrix}
2(p-1)=p
\therefore\; p=2
と、k を介さずにすぐに求まります。
ちょっとした工夫
\begin{pmatrix}p-1\\p\end{pmatrix} = k\begin{pmatrix}2\\4\end{pmatrix}
をそのまま平行記号にすると
\begin{pmatrix}p-1\\p\end{pmatrix} /\! / \begin{pmatrix}2\\4\end{pmatrix}
ですが、
\begin{pmatrix}2\\4\end{pmatrix} /\! / \begin{pmatrix}1\\2\end{pmatrix}
なので、
\begin{pmatrix}p-1\\p\end{pmatrix} /\! / \begin{pmatrix}1\\2\end{pmatrix}
としています。このような工夫をサラッとできると計算が楽に、またミスも少なくできます。
垂直問題

内積 =0
垂直とくればほとんど反射的に内積がゼロ、と行きましょう。先の例題を垂直版に焼き直して使い方を見てみます。
\triangle\mathrm{PAB}=90^\circ のとき \mathrm{P} の座標を求めよ。

\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AP}}=0
より、
\begin{eqnarray} \begin{array}{c} \begin{pmatrix}1\\2\end{pmatrix}\cdot\begin{pmatrix}p-1\\p\end{pmatrix}=0\\ (p-1)+2p=0\\ \therefore\; p=\displaystyle\frac{1}{3} \end{array} \end{eqnarray}
よって、
\mathrm{P}(\displaystyle\frac{1}{3},\,\displaystyle\frac{4}{3})
ここも、ちょっとした工夫を施しています。
角度問題

内積を使って角度を求める
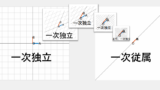
角度を求めよ、ときたら↓の記事の「内積の図形的意味」で述べたこの関係式を用います。
\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}=|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|\cos\theta
例えば次の例題を考えます。
角度 \theta を求めよ。

\begin{eqnarray} \overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}} &=& |\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|\cos\theta\\ \begin{pmatrix}1\\\sqrt{3}\end{pmatrix}\cdot\begin{pmatrix}\sqrt{3}\\1\end{pmatrix} &=& \left|\begin{pmatrix}1\\\sqrt{3}\end{pmatrix}\right|\left|\begin{pmatrix}\sqrt{3}\\1\end{pmatrix}\right|\cos\theta\\ 2\sqrt{3} &=& 2\cdot 2\cdot\cos\theta\\ \cos\theta &=& \frac{\sqrt{3}}{2}\\ \therefore\;\theta &=& \frac{\pi}{6} \end{eqnarray}
この問題の場合は図形的解釈でも \theta=\displaystyle\frac{\pi}{6} が分かりますが、ベクトルを使うメリットはそのような図形的解釈を持ってこなくても解けることです。
大きさ問題

2乗する
大きさを求めるには2乗します。その際、2乗するベクトルを素性の分かっているベクトルで表現します。この例↓では、|\overrightarrow{\mathrm{AB}}| を求めたいので |\overrightarrow{\mathrm{AB}}|^2 としますが、素性が分かっているのは \overrightarrow{\mathrm{OA}} と \overrightarrow{\mathrm{OB}} です。
\overrightarrow{\mathrm{AB}} の大きさを求めよ。

\begin{eqnarray} |\overrightarrow{\mathrm{AB}}|^2 &=& |\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}|^2\\ &=& |\overrightarrow{\mathrm{OB}}|^2-2\times\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}+|\overrightarrow{\mathrm{OA}}|^2\\ &=& 4-2\times 2\cdot 2\cdot\cos 30^\circ+4\\ &=& 8-4\sqrt{3}\\ &=& 2\,(\sqrt{3}-1)^2 \end{eqnarray}
\therefore\;|\overrightarrow{\mathrm{AB}}|=\sqrt{2}\,(\sqrt{3}-1)\quad (>0)
ハタと気づきませんか?:余弦定理
余弦定理とは、三角形に対して成り立つ次の公式です。
\mathrm{AB}^2=\mathrm{OA}^2+\mathrm{OB}^2-2\cdot\mathrm{OA}\cdot\mathrm{OB}\cdot\cos\theta

これはまさに、上で求めた式変形そのものですね。
余弦定理については↓の記事で詳しく扱っています。
三角形の面積問題

公式
公式は↓ですが、わざわざ覚える必要もないです。
S = \frac{1}{2}\sqrt{|\overrightarrow{\mathrm{OA}}|^2|\overrightarrow{\mathrm{OB}}|^2-(\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}})^2}

覚える必要もない
覚える必要もないというのも、普通に、
底辺 \times 高さ \div 2
をすればよいので。すなわち、底辺を \overrightarrow{\mathrm{OA}} と見れば高さは、
\begin{eqnarray} \text{高さ} &=& |\overrightarrow{\mathrm{OB}}|\,\sin\theta\\ &=& |\overrightarrow{\mathrm{OB}}|\,\sqrt{1-\cos^2\theta} \end{eqnarray}
なので、
\begin{eqnarray} S &=& |\overrightarrow{\mathrm{OA}}|\times|\overrightarrow{\mathrm{OB}}|\,\sqrt{1-\cos^2\theta}\div 2\\ &=& \frac{1}{2}\sqrt{|\overrightarrow{\mathrm{OA}}|^2|\overrightarrow{\mathrm{OB}}|^2-(|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|\cos\theta)^2}\\ &=& \frac{1}{2}\sqrt{|\overrightarrow{\mathrm{OA}}|^2|\overrightarrow{\mathrm{OB}}|^2-(\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}})^2} \end{eqnarray}
となり、覚えるまでもなく素直に計算すればそのようになります。
あえて覚えるには:公式の気持ちを理解する
まず、三角形の面積なのでそれは
\begin{eqnarray} S &=& \frac{1}{2}|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|\\ &=& \frac{1}{2}\sqrt{|\overrightarrow{\mathrm{OA}}|^2|\overrightarrow{\mathrm{OB}}|^2} \end{eqnarray}
っぽい感じになるよね、と理解します。
そして、実際には直角でなければこの面積より小さいので、負の補正が必要になり、
S = \frac{1}{2}\sqrt{|\overrightarrow{\mathrm{OA}}|^2|\overrightarrow{\mathrm{OB}}|^2-〇〇}
となるはずで、問題は〇〇がどうなるかです。
ここには角度よって変化する値が入るはずなので、そうだ内積だと思い出します。しかも、|\overrightarrow{\mathrm{OA}}|^2|\overrightarrow{\mathrm{OB}}|^2 と次元は同じはずなので2乗が必要であると理解して、
S = \frac{1}{2}\sqrt{|\overrightarrow{\mathrm{OA}}|^2|\overrightarrow{\mathrm{OB}}|^2-(\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}})^2}
を思い出すことができます。
その際、
\sin\theta = \sqrt{1-\cos^2\theta}
が頭をよぎればこれで完璧だと自身も深まるはずです。
まとめ
平面ベクトルの解法の全体像を見てきました。それは下記↓の図のようになります。

ベクトルの利点は、図形的なひらめきをあまり持たなくても計算で処理できるようにしてくれるところです。デメリットはその分計算量が多くなることですが、機械的にできる部分なので練習しましょう。受験を乗り越えれば計算はコンピュータに任せればよいです。

コメント