【テニスの物理】空気抵抗とマグヌス効果　慎重に打つと逆に入らない謎　スピンの威力　野球にも応用ができる計算の実例

　バックアウトしたくないので慎重に打つとむしろバックアウトし、しっかりと打った方が逆にしっかりとコートに収まる経験をしたことはありませんか？確かにそうなのです。その理由は空気抵抗とマグヌス効果にあります。

この記事を読めばそれらの効果を運動方程式とシミュレーションで理解でき、明日からしっかりと打とうという気になります。

空気抵抗は速度の2乗に比例して抗う

空気抵抗

　直前の記事↓では空気抵抗は無いとして計算をしました。

大学入試問題ではほとんどの場合、簡単のためにこの条件下で問題が出てきますが、現実世界には空気抵抗があります。

空気抵抗は、物体の速度が遅い場合には速度の1乗に比例しますが、速度が速くなると2乗に比例します。自動車の燃費を計算する↓の記事でも2乗に比例するとして計算しました。

ここでも全く同じです。空気抵抗は次の式で表されます。

$$\begin{eqnarray} F_{air} &=& C_d\frac{1}{2}\rho A\cdot v^2\\ &=& 9.5182\times 10^{-4}\cdot v^2 \end{eqnarray}$$

となります。定数値の計算は次に示しますが、飛ばしてよいです。ここで重要なのは空気抵抗 $F_{air}$ は速度の2乗 $(v^2)$ に比例するということです。

定数値

　$C_d$ は空気抵抗係数、$\rho$ は空気密度、$A$ は投影面積、$v$ は速度です。

空気抵抗係数 $C_d$ は計算サイトにより計算すると、ボールの直径に $0.068\mathrm{[m]}$, 速度を仮値として $30\mathrm{[m/s]}$ を入れて、

$$C_d = 0.435$$

という値が得られます。

空気密度 $\rho$ はおおよそ

$$\rho = 1.205\mathrm{[kg/m^3]}$$

です。

投影面積 $A$ はボールの半径を $0.034\mathrm{[m]}$ として、

$$A=\pi\cdot 0.034^2\mathrm{[m^2]}$$

です。

これらより定数値は

$$\begin{eqnarray} C_d\frac{1}{2}\rho A &=& 0.435\times\frac{1}{2}\times 1.205\times\pi\times 0.034^2\\ &=& 9.5182\times 10^{-4} \end{eqnarray}$$

となり、空気抵抗の計算ができます。ただし、空気抵抗が働く力の向きは速度と反対の向きです。そのことに注意して運動方程式を立てます。

運動方程式

　運動方程式はベクトルで書くと

$$m\overrightarrow{a} = \overrightarrow{F_g} + \overrightarrow{F_{air}}$$

です。

$\overrightarrow{F_g}$ は重力なので成分表示すれば $m\begin{pmatrix}0\\-g\end{pmatrix}$ です。

$\overrightarrow{F_{air}}$ は空気抵抗で大きさは先に見たように

$$C_d\frac{1}{2}\rho Av^2$$

ですが、向きをどう持たせるかです。速度 $\overrightarrow{v}$ と逆向きにしたいので、次のようにします。

$$\overrightarrow{F_{air}} = -C_d\frac{1}{2}\rho A|\overrightarrow{v}|\overrightarrow{v}$$

右辺に負号がついていることに注意してください。これにより $\overrightarrow{v}$ と逆の向きを表します。よって、運動方程式は

$$m\begin{pmatrix}a_x\\a_y\end{pmatrix}=m\begin{pmatrix}0\\-g\end{pmatrix}-C_d\frac{1}{2}\rho A\sqrt{v_x^2+v_y^2}\begin{pmatrix}v_x\\v_y\end{pmatrix}$$

となります。

シミュレーション1. $v=15\mathrm{[m/s]}$

　実際に数字を入れて計算します。仰角 $\theta=30^\circ$ 、打球速度 $v=15\mathrm{[m/s]}(=54\mathrm{[km/h]})$ で打った場合です。結構緩く打った場合に相当します。

空気抵抗が無い場合には $20\mathrm{[m]}$ まで飛びましたが、空気抵抗を考慮すると $16.5\mathrm{[m]}$ と短くなりました。

グラフ中にはボールにかかる力を記載しました。赤の線は重力であり、ボールの重さそのもの（$60\mathrm{[gf]}$）です。それに対して空気抵抗は $21.8\mathrm{[gf]}$ かかっており、この場合でもボールの重さの1/3程度の力がかかっています。この力により減速され、距離が縮みます。ちなみに、相手コートにバウンドする瞬間には速度は $12.0\mathrm{[m/s]}$ になっており、初速度 $15\mathrm{[m/s]}$ に対して $8$ 割程度に落ちています。

シミュレーション2. $v=30\mathrm{[m/s]}$

　次は打球速度を $v=30\mathrm{[m/s]}(=108\mathrm{[km/h]})$ とします。これは、中級から中上級くらいの人がしっかりと打った時の打球速度でしょうか。ぬいさんぽさんの動画では一般人で $118\mathrm{[km/h]}$、ぬいさんぽさんで $134\mathrm{[km/h]}$ 出ていました。

今度は $44.8\mathrm{[m]}$ 飛びました。空気抵抗が無い場合には $80\mathrm{[m]}$ 飛びます（$20\mathrm{[m]}$ の4倍）から、ずいぶんと短くはなりました。空気抵抗の大きさを確認すると、打った瞬間には $87.0\mathrm{[gf]}$ であり、ボールの重さ以上の力がかかっていることが分かります。これは、$v=15\mathrm{[m/s]}$ のときの空気抵抗が $21.8\mathrm{[gf]}$ だったので $4$ 倍です。速さが $2$ 倍になったので空気抵抗は $4$ 倍となり、ぐっとアウトしにくくなります。

しかしながらまだバックアウトはしています。スピンを掛けない場合、バックアウトします。

スピンを掛けると急速に落ちる

マグヌス力

　次にスピンを掛けたときの運動方程式を考えます。スピンを掛けるとマグヌス力が働きます。この動画↓はマグヌス効果が非常によくわかる動画です。バックスピンを掛けて落としたバスケットボールはその軌道を大きく変えて落下します。

マグヌス力は流速に対して（従って無風の場合はボールの進行方向に対して）垂直に働きます。その大きさはボールの速さ $v\mathrm{[m/s]}$ （無風を考える）と回転速度 $\omega\mathrm{[rad/s]}$ の積に比例し、$F_{magnus}=Sv\omega$ と書けます。比例定数 $S$ の値はこの解説書を参考に $S=0.00023$ としました。解説書にも値が記載されていましたが、なぜかその中に記載されている図と合わなかったため、図と合うように値を調整しました。

従って、ベクトルの成分でマグヌス力を表すと

$$\overrightarrow{F_{magnus}} = S\omega\begin{pmatrix}v_y\\-v_x\end{pmatrix}$$

となります。

運動方程式

従って運動方程式は、

$$m\begin{pmatrix}a_x\\a_y\end{pmatrix}=m\begin{pmatrix}0\\-g\end{pmatrix}-C_d\frac{1}{2}\rho A\sqrt{v_x^2+v_y^2}\begin{pmatrix}v_x\\v_y\end{pmatrix}+S\omega\begin{pmatrix}v_y\\-v_x\end{pmatrix}$$

となります。

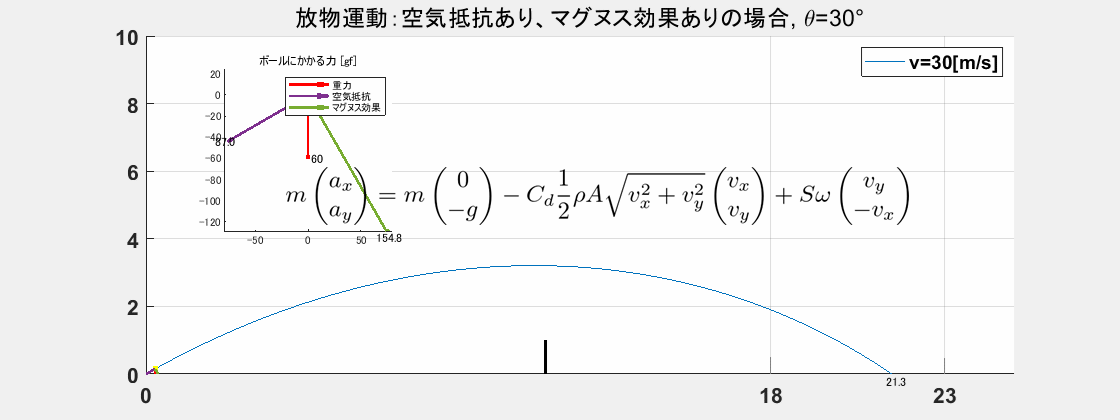
シミュレーション3. $v=30\mathrm{[m/s]}$, $\mathrm{rps}=35$

　回転数を秒速 $35$ 回転($\mathrm{[rps]}$)としてみます。運動方程式の $\omega$ の単位は角速度 $\mathrm{[rad/s]}$ なので、$\omega=35\times 2\pi\mathrm{[rad/s]}$ です。先のぬいさんぽさんの動画でぬいさんぽさんは秒速 $44$ 回転です。$35$ 回転は中級から中上級者くらいの回転量でしょうか。

このときボールは $21.3\mathrm{[m]}$ に落下し、ベースラインを超えていないです。マグヌス力は実にボールの重さの $2$ 倍程度も働いています。しかも、落下する際には力の方向は手前側に向いており、よりアウトしない側に力が働いています。この力によりスピンのかかったボールはベースライン近くでグイっと落ちてインになるのです。

フラットで強打するとアウトする

　スピンをかけると急速に落ちるのと反対に、バックスピンをかければなかなか落ちてこないことは想像に難くないですし、また経験上もそうですよね。

シミュレーション4. $v=30\mathrm{[m/s]}$, $\theta=0^\circ$, $\mathrm{rps}=-10$

　実際この図↓はどちらも球速は同じ $v=30\mathrm{[m/s]}$ ですが、青の方にはスピンが毎秒 $10$ 回転かかっているのに対し、赤の方はバックスピンが毎秒 $10$ 回転かかっています。より現実に近しいシミュレーションにするため、打ち出す高さを $1.5\mathrm{[m]}$ としました。そして、打ち上げ角度を赤の方は $0°$ にしてみましたが、バックスピンの効果でボールが伸び、アウトしてしまいます。

バックスピンをかけているから当然だよね、と思うかもしれませんが、意図せずともバックスピンがかかってしまう場合があります。それが、フラットで打った場合です。

フラットで打つとバックスピンがかかってしまう

　相手から飛んでくるボールはバウンド後には必ずスピンがかかります。スピンがかかっているボールに対してラケットをフラットに当てると跳ね返った後はバックスピンがかかります。下の図はテクニカルテニス¹という本に記載されいた図の引用ですが、毎分 $3,820$ 回転（＝毎秒 $64$ 回転）のトップスピンで迫ってくるボールをフラットで打ち返した場合、毎分 $1,530$ 回転（＝毎秒 $26$ 回転）のバックスピンがかかると述べられています。

テクニカルテニス

跳ね返りの角度も $6.5^\circ$ ついてしまうため、これを抑えようとラケット面をかぶせると、それはそれで今度はネットのリスクも高まってしまいます。

従って、基本はスピンをかけてネットの高いところを通す、というのがよさそうです。

まとめ

　空気抵抗とマグヌス効果について考えました。この効果によりボールはアウトしにくくなります。

特にマグヌス力は時としてボールの重力よりも大きな力のため、これの有りと無しとでは大違いであることを理解しました。ここに、慎重に打つがあまり当てるだけになってしまうと逆にアウトしてしまう理由があります。もちろん、しっかりとスピンをかける技術が必要です。

また、フラットで強打するとアウトしてしまう理由も分かりました。フラットに当てすぎると意図せずバックスピンがかかってしまうためです。

従って、スピンの技術を習得し、そしてしっかりと打つことが重要ですね。

発展：シミュレーションってどうやっているの？

　シミュレーションは意外に簡単です。それに加えて微分や積分の本質的な感覚も同時に理解できてしまうので、ここで説明しようと思います。微分や積分の本質的な感覚とは具体的には、微分の $\displaystyle\frac{dy}{dx}$ は分数っぽい感覚であるとか、積分は細かい短冊の寄せ集めであるとかいった感覚で、↓の記事で述べています。

運動方程式は微分方程式

　運動方程式を再掲します。

$$m\begin{pmatrix}a_x\\a_y\end{pmatrix}=m\begin{pmatrix}0\\-g\end{pmatrix}-C_d\frac{1}{2}\rho A\sqrt{v_x^2+v_y^2}\begin{pmatrix}v_x\\v_y\end{pmatrix}+S\omega\begin{pmatrix}v_y\\-v_x\end{pmatrix}$$

シミュレーション的には $x$ も $y$ も同様の操作なので、ここでは $y$ に注目して述べます。なぜ $x$ でなく $y$ にしたかは、重力成分も含めた方が（ややこしくはなるが）分かりやすいと思ったからです。

$y$ 成分のみ書き出してみる

　両辺を $m$ で割り $y$ 成分のみ書き出します。$a_y=\displaystyle\frac{dv_y}{dt}$ なので、

$$\frac{dv_y}{dt} = -g-\frac{C_d\rho A\sqrt{v_x^2+v_y^2}}{2m}v_y-\frac{S\omega}{m} v_x$$

$$\therefore\; dv_y = \left(-g-\frac{C_d\rho A\sqrt{v_x^2+v_y^2}}{2m}v_y-\frac{S\omega}{m}v_x\right)\cdot dt$$

コンピュータに繰り返し計算をさせる

　ここで $dt$ をいくらにするか設定します。私は $dt=0.01$ として計算しました。この幅が「細かい短冊」の幅です。細かい方が誤差は小さいですが計算時間が多くかかります。

あとは漸化式のように次々と値が求まっていきます。$v_y$ の初期値は $v_0\sin\theta=30\sin 30^\circ=15$、$v_x$ の初期値は $v_0\cos\theta=30\cos 30^\circ=25.98$ なので、その他の定数も入れると、

$$\begin{eqnarray} dv_y &=& \left(-9.8-\frac{0.435\times 1.205\times (\pi\cdot 0.034^2)\times\sqrt{25.98^2+15^2}}{2\times 0.06}15-\frac{0.00023\times (2\pi\cdot 35) \times 25.98}{0.06}\right)\times 0.01\\ &=& -0.3884 \end{eqnarray}$$

より $dt$ 秒後の速度 $v_y$ は、

$$v_y = 15-0.3884=14.6116$$

と求まります。同様に $v_x$ は

$$v_x = 25.9836$$

と求まるため、これらを使って次の $dt$ 秒後の速度を求めます。これを繰り返して $dt$ 秒間隔での速度 $v_x$, $v_y$ を求めます。

速度が分かれば位置も同様にして求められる

　速度が分かったので位置も同様にして求められます。すなわち、初期位置は $x=0$, $y=0$ で、初期速度は $v_x=25.98$, $v_y=15$ なので、$dt$ 秒間の変位 $dx$, $dy$ は

$$\begin{eqnarray} dx &=& v_x\, dt = 25.98\times 0.01 = 0.2598\\ dy &=& v_y\, dt = 15\times 0.01 = 0.15 \end{eqnarray}$$

より、位置は

$$\begin{eqnarray} x &=& 0 + 0.2598 = 0.2598\\ y &=& 0 + 0.15 = 0.15 \end{eqnarray}$$

と求められ、これらを元に次の $dt$ 秒後の位置を求め、それを繰り返します。

微分は分数、積分は細かい短冊の寄せ集め

　微分は分数の感覚です。$a_y=\displaystyle\frac{dv_y}{dt}$ なので、

$$dv_y = a_y\, dt$$

として $dv_y$ を求めます。これは幅 $dt$ の短冊です。そしてそれを足していって、$v_y$ を求めます。このように、プログラム自体はいたって単純です。

関連記事

　最後まで読んでいただいたあなたにはぜひこちらの記事も読んでいただきたいです。

↓は、運動量と力積の関係を使った記事です。

↓は、運動量保存の法則と跳ね返り係数の式を使った記事です。

1. テクニカルテニス Rod Cross, Crawford Lindsey; 常盤 泰輔訳, p157 ↩︎