テニスでの得失点は、少なくともレクリエーションプレイヤーレベルだと自分が素晴らしいショットをして得点するよりも、ミスをして失点をするケースの方が圧倒的に多いです。ネットかアウトということですが、ここでは高校物理の初めの方に習う放物運動を使ってバックアウトしない条件を求めてみます。
実際には空気抵抗があるのですが、ここではまずは簡単のために空気抵抗は無いこととします。空気抵抗がある場合は高校物理の範囲を超えますので別記事↓にしています。
自分が打つ場合にコートに収める
ベースラインから仰角 θ=30∘ でショットする。サービスラインを超え、バックラインを超えない範囲に落とすための打球速度 v0 の範囲は?
簡単のため、高さ 0[m] から打つとする。

問題文の絵にあるように、v0=15[m/s] で打つと x=20[m] に落下するので条件を満たします。
解. θ のままで求める
等加速度運動の公式より
x=v0cosθ⋅ty=v0sinθ⋅t–12gt2
参考に下記の記事↓では等加速度運動の公式の完全理解を目指しています。
サービスラインを超える条件
x=18 となる時刻 t1 は、
18=v0cosθ⋅t1∴t1=18v0cosθ
これを y の式に入れ、y>0 ならよいので、
y=v0sinθ⋅18v0cosθ−12g(18v0cosθ)2>0
∴v0>√18g2sinθcosθ=√18gsin2θ
ベースラインを超えない条件
x=23 となる時刻 t2 は、
23=v0cosθ⋅t2∴t2=23v0cosθ
これを y の式に入れ、y<0 ならよいので、
y=v0sinθ⋅23v0cosθ−12g(23v0cosθ)2>0
∴v0<√23g2sinθcosθ=√23gsin2θ
実際どの程度? θ=30∘ を代入する
g=9.8[m/s2], θ=30∘ を代入すると、
サービスラインを超えるためには
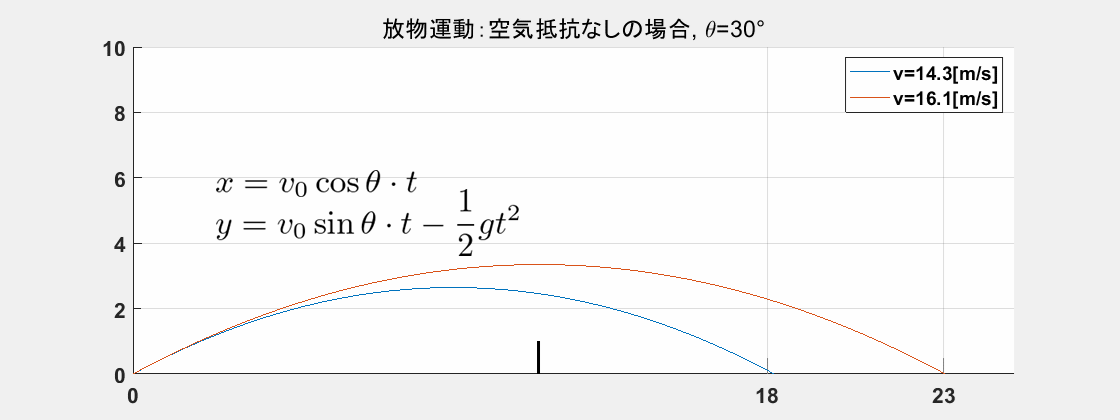
v0>√18g2sinθcosθ=14.3[m/s]
ベースラインを超えないためには
v0<√23g2sinθcosθ=16.1[m/s]
実際、グラフを書かせると下図のようになります。

14.3[m/s] は時速に直すと
14.3[m/s]=14.3×3.6[km/h]=51.48[km/h]
同様に、16.1[m/s] は
16.1[m/s]=16.1×3.6[km/h]=57.96[km/h]
です。
相手が打つ場合にアウトボールをウォッチする
同じようなことですが今度は逆の立場を少しだけ考えてみます。相手が打ったボールがアウトする場合にはウォッチしたいですが、それを見極める原理原則です。
相手が打ったボールは空気抵抗が無ければ放物運動をします。放物運動は頂点に対して左右対称です。従って、アウトになるかどうかを見極めるためにはボールの頂点に着目します。つまり相手が打つときに逆算しておいて、
- 相手がボールを打つ地点とベースラインの中間地点
をイメージします。この中間地点よりも頂点が超えそうならアウトするだろうと判断するわけです。
しかしながら実際には
- 実際には空気抵抗があること
- 実際にはスピンがかかっていること
がこれまでの原理原則とは異なります。
空気抵抗があることによりボールは必ず少し手前側に落ちます。従って、目印とする想定頂点を少しだけ手前にします。また、スピンがかかっていることにより、それが順スピンならかなり手前に落ちますし、逆スピンならかなり伸びます。また、実際には相手の打点は地上 0[m] ではないので、この点も考慮が必要です。
これらの調整は必要で、練習のポイントになろうかと思います。しかし逆に言えば、まずは原理原則を押さえることで、練習のポイントをその後段の微調整ポイントに集中させることができれば、より効率的にマスターできると思います。
まとめ
空気抵抗が無い場合のバックアウトをしない条件を求めました。等加速度運動の公式:
x=v0cosθ⋅ty=v0sinθ⋅t–12gt2
を解き、角度 θ とした場合、
√18gsin2θ<v0<√23gsin2θ
と求まりました。角度を θ=30∘ で計算すると、
14.3[m/s]<v0<16.1[m/s]
(51.48[km/h]<v0<57.96[km/h])
です。結構遅い球ですね。空気抵抗が無いとしたため、このような計算結果になった側面があります。↓の記事で空気抵抗がある場合を考えます。
また、相手のアウトボールを確実にウォッチする原理原則を述べました。ボールは空気抵抗が無ければ放物運動をするので、相手の打点と自分のベースラインの中間地点と頂点を比べることでまずはアウトかどうかを判断します。実際には空気抵抗やスピンなどがあるのでそれに合わせて微調整をして最終判断をします。




コメント