格子定数と明線角度の公式
格子定数 $d$ の回折格子に波長 $\lambda$ の波が来た場合、明線になる角度 $\theta$ の公式は次のようです。
$$d\sin\theta_n = n\lambda$$
ここで、格子定数 $d$ が
- 小さくなる
と明線角度は
- 狭くなるでしょうか
- 広くなるでしょうか
答えは、
- 広くなる
です。
それは式を見れば理解が可能ですが、いちいち式を見ずともイメージで理解できるようになると楽です。
イメージアニメーション その1
アニメーション
波源が狭くなったり広くなったりした場合に干渉がどのようになるのかを計算してアニメーションにしました。
中央の絵が干渉した結果を上から見たもので、左側の絵は波源付近の拡大図です。そして右側の絵は $L=1000$ での振幅です。青線はある瞬間の波形で赤線はその振幅です。このあたりの絵の意味は、#2の記事↓で確認できます。
波長が変わる場合も同様に考える
ここでは格子定数の方を動かしましたが、逆に格子定数を固定して波長を変えても同様です。
例えば
- 波長が短くなる（可視光では青色）
ということは、
- 相対的に格子定数が大きくなるのと同義
なので、
- 明線角度は狭くなる
わけです。つまり、
白色光を入れると、青の光が中央付近に、赤の光が外側に現れる
ということです。
波長を変えて入射した場合の実像例
ここでも山形大学のHPを引用して写真を載せます。波長を変えると表現しましたが、実際には白色光を入射しています。白色光は様々な波長の混ぜ合わせだからです。
課題２ 回折格子 (yamagata-u.ac.jp)
イメージアニメーション その2
こちらの方が実践的かもしれません。明線の式
$$d\sin\theta = n\lambda$$
をそのままイメージする感じです。$n=1$ のみ取り出して考えます。
波長固定で格子定数を変化させる
波長は固定で格子定数を変化させます。1波長の光路差ができるためにどれだけの角度 $\theta$ が必要か、というイメージです。
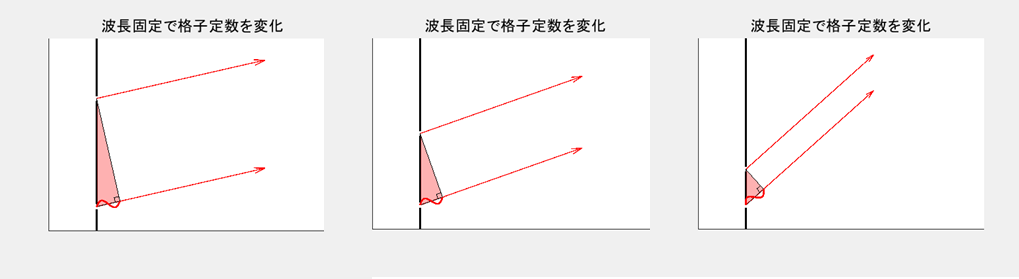
静止画で確認
いくつかのポイントを静止画で確認します。格子定数が狭いと1波長の差を生むためによりたくさんの角度が必要なことがイメージできると思います。
格子定数固定で波長を変化させる
今度は波長を変化させます。青の方が中央寄りに明線ができるイメージをさらに強固にしてください。
静止画で確認
いくつかのポイントを静止画で確認します。波長が長いと1波長の差を生むためによりたくさんの角度が必要なことがイメージできると思います。波長に押し出される感じですね。
まとめ
格子定数と波長を変化させたときに明線の角度がどのように変化するかをイメージしました。この中で最もイメージしやすいのは、私自身は最後の「格子定数固定で波長を変化」なのですが、皆さんはどうですか？波長に押し出されるイメージを持って理解しています。
このようにイメージができるようになると、とっさに
青は中央よりか外側か？
といったような問いかけにも自信を持って答えられるようになります。
コメント