【微分は何のため？】基本はグラフを書くために使う：かっこのままで微分する裏技 や 導関数の線形性のイメージ も紹介

　高次のグラフを書くときに微分をします。そのことをイメージでつかみます。また、かっこの何乗とかになっていると展開が面倒ですが、展開せずにかっこのままで微分してしまう裏技を紹介します。

微分は何のため？→高次のグラフを書く

問題：$y=x^3-3x+1$ のグラフを書け

　次の問題を考えます。

微分で高次のグラフが書けるイメージ

　微分は接線の傾き、もしくは超拡大したときのグラフの傾きを表します。微分すると、

• $y^{\prime}=3x^2-3$

となります。各 $x$ でのこの値は元の関数 $y=x^3-3x+1$ の接線の傾きを表します。これらの関係を動画にすると下図の通りです。

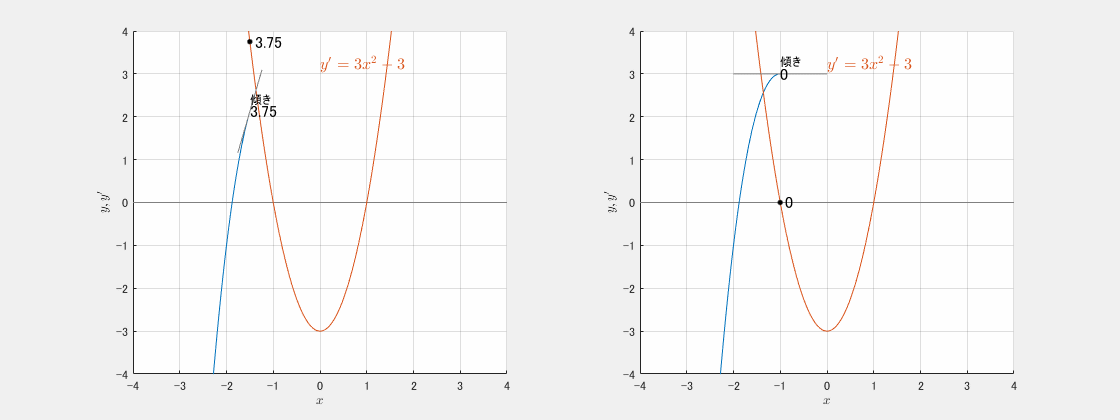
　適当な $x$ で止めて考えます(下図)。

　赤のグラフが導関数ですが、その値が青のグラフの傾きになっています。

この両者の関係が理解できれば、微分の問題はお手の物です。特に動画が一瞬止まるところが大事で、

の関係をしっかりとイメージしたいです。

鋭い指摘

　ところで、次のように思った人は、なかなか鋭いです。

• 青のグラフはその形（増減の様子）は分かっても、上下の絶対的な位置は不定なのでは？

この動画のようなイメージです。これは、元のグラフの少なくとも1点を与えることにより定まります。

動画では $x=0$ のときに $y=1$ であることを用いて定めました。

微分情報だけでは不定

　このように、微分式 $y^{\prime}$ だけから元の式 $y$ を求めると不定な状態になります。この不定な状態を脱するためには元の式 $y$ の少なくとも一点どこを通るのかの情報を付加する必要があります。

これに近しい問題が2025年度の共通テストに出ていました。なんてことない問題ですので、確実に取りたい部分です。（第3問：微分積分）

かっこのままで微分する裏技→平行移動を利用：合成関数の微分

　ここでは、

• $y=(x-1)^5$

を楽々微分することを目的にします。そのため、まずは簡単な例として

• $y = (x-1)^2$

を用いて素直な解き方と合成関数の微分の入り口の解き方の両方を行い、両者が一致することを確かめます。さらに、

• $y=(2x-1)^2$

も同様に考えられることを示します。これと同じ問題を↓の記事ではより一般化して説明しており、合成関数の微分が身に付きます。

該当箇所に直接ジャンプ→$y=(2x-1)^2$ の微分 かっこのままで微分する

$y=(x-1)^2$ の微分

素直な解き方：展開して微分

　素直に解くには展開です。展開すると、

• $y=x^2-2x+1$

なので、これを微分して、

• $y^{\prime}=2x-2$

です。

かっこのままで微分：平行移動を利用

　下図最左の赤のグラフ：$y=(x-1)^2$ は青のグラフ：$y=x^2$ を右に1だけ平行移動したグラフです。つまり、例えば $y=(x-1)^2$ を $x=2$ で微分した値は、$y=x^2$ を $x=1$ で微分した値と同じです（下図最右は中央と同じ）。この関係は任意の $x$ で成り立つので、$y=(x-1)^2$ を微分した値は、$y=x^2$ を微分した $y^{\prime}=2x$ の $x$ の値を1だけ調整すればよく、$y^{\prime}=2(x-1)$ となります。実際、先ほどの具体例である $x=2$ を入れると分かりますよね、$y^{\prime}=2(x-1)$ の $x$ に $2$ を入れた場合と、$y=x^2$ の微分である $y^{\prime}=2x$ の $x$ に $1$ を入れた場合とが同じ $y^{\prime}=2$ になることが。

改めて書くと、

であり、展開して求めたものと一致します。

　ただし注意点は、このように考えることができるのは $x$ の係数が1のときだけです。$x$ の係数が1ではないときは単なる平行移動ではないからです。この場合の考え方は【合成関数の微分】の記事↓で取り扱います。

とは言いつつ、無理やり平行移動の形に式変形することで同じように考えることができます。例えば、$y=(2x-1)^2$ の微分を次に考えてみましょう。

$y=(2x-1)^2$ の微分

　次のように式変形すれば、平行移動とみなせます。

• $y=4\left(x-\displaystyle\frac{1}{2}\right)^2$

これは、$y=4x^2$ を右に $\displaystyle\frac{1}{2}$ だけ平行移動したグラフです。従って、

• $y^{\prime}=4\cdot2\left(x-\displaystyle\frac{1}{2}\right)$

となります。展開して微分して一致を確認してみてください。

　せいぜい2乗なら展開してもそれほど苦はないでしょうが、もっと高次になると展開するのは苦労するので、この考え方は重宝します。重宝する例を次の $y=(x-1)^5$ で確認しましょう。

$y=(x-1)^5$ の微分

　　ここまで高次になると展開するのはうんざりします。しかし、$y=x^5$ の微分は簡単であり $y=5x^4$ です。$y=(x-1)^5$ は $y=x^5$ を右に一つ平行移動したものに過ぎないので、微分したものも同じように右に一つ移動したものとなります。従って、

• $y^{\prime} = 5(x-1)^4$

となることが理解できます。

　さらに詳しくは↓の記事で取り上げています。ここでは微分の連鎖律をイメージで理解することを目的にしています。

導関数の性質の一つ、線形性のイメージ

　最後に、導関数の性質の一つに「線形性」がありますが、微分のイメージが「超拡大したら直線」であることを考えれば線形性は当然に思えてきます。

　2つの関数 $f(x), g(x)$ と定数 $k$ について、以下の性質が成り立ちます。

実は、最初の問題で

$$y=x^3-3x+1$$

の微分をし、それが

$$y^\prime = 3x^2-3$$

と求めましたが、ここに線形性の性質を用いています。

$y=kf(x)$ ならば、$y^{\prime}=kf^{\prime}(x)$

　ここでは具体的に、

• $k = 3$
• $f(x) = x^2$

すなわち、

• $y = kf(x) = 3x^2$

の微分を考えます。

具体的に $x=1$ での傾きを考えます。それを図示すると下の図のようです。

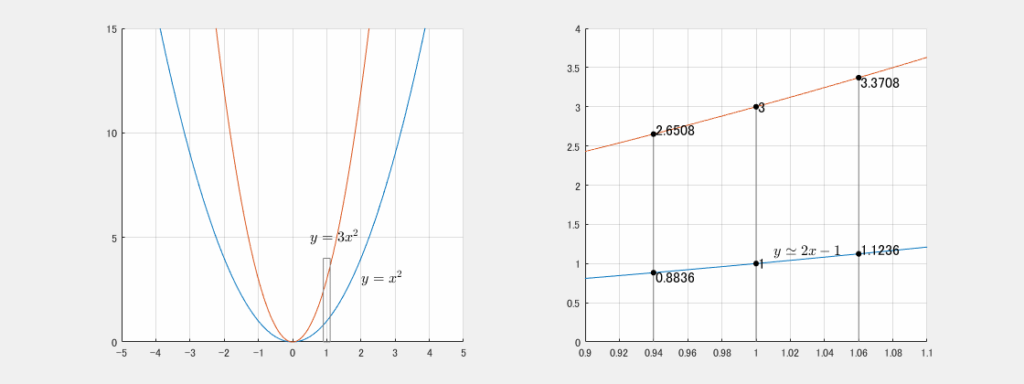
右のグラフは左のグラフの四角部分です。赤のグラフは常に●●青のグラフの3倍です。

右側の青のグラフはほぼ直線であり、それは
$$y\simeq 2x-1$$
です。

赤のグラフは常に●●青のグラフの3倍なので、右側の赤のグラフは
$$y\simeq 6x-3$$
となるはずです。

当然ながら、傾きは3倍です。

つまり、赤の $kf(x)$ の微分係数（直線の傾き）は、元の関数である青の $f(x)$ の微分係数の $k$ 倍になっています。

　以上のように、「曲線も超拡大したら直線（線の形）」なのだから、導関数には線形の性質が成り立つわけです。

$y=f(x)\pm g(x)$ ならば、$y^{\prime}=f^{\prime}(x)\pm g^{\prime}(x)$

　$\pm$ の記号はそれぞれで成り立つことを示しています。すなわち、

• $y=f(x)+g(x)$ ならば、$y^{\prime}=f^{\prime}(x)+g^{\prime}(x)$
• $y=f(x)-g(x)$ ならば、$y^{\prime}=f^{\prime}(x)-g^{\prime}(x)$

であり、それらをまとめて記載しています。$+$ も $-$ もどちらも同じことなので、ここでは $+$ の方だけを考えます。具体的には、

• $y = f(x) = x^2$
• $y = g(x) = x$

を考え、その和である

• $y = f(x)+g(x) = x^2+x$

の微分を考えます。

具体的に $x=1$ での傾きを考えます。それを図示すると下の図のようです。

右のグラフは左のグラフの四角部分です。黄色のグラフは常に●●青のグラフと赤のグラフの和です。

右側の青のグラフと赤のグラフはほぼ直線(赤のグラフは正真正銘の直線)であり、それらはそれぞれ
$$\begin{eqnarray} y&\simeq& 2x-1\\ y&=&x \end{eqnarray}$$
です。黄色のグラフは常に●●青のグラフと赤のグラフの和なので、
$$y\simeq 3x-1$$
となるはずです。

当然ながら、傾きは2直線の傾きの和です。

つまり、黄色の $f(x)+g(x)$ の微分係数（直線の傾き）は、元の関数である青の $f(x)$ と赤の $g(x)$ の微分係数の和になっています。

　以上のように、「曲線も超拡大したら直線（線の形）」なのだから、導関数には線形の性質が成り立つわけです。

まとめ

　微分を習い始めたころは、微分っていったい何に使うのだろうか？と感じると思います。基本は高次のグラフを書くために使います。その際、かっこの何乗とかになっているものは展開せずにかっこのままで微分するテクニックを身につければ、計算が非常に楽にできます。

おススメ内部リンク記事