【角の二等分線からの発想#1】線分比 と 二等辺三角形 に着目してみよう

　角の二等分線を見たときにまず考えたい発想は線分比です。他には、二等辺三角形が隠れている場合がある、という発想です。ここでは単純な問題によりその発想を養います。

ここの単純な問題で発想が養われた方は、上級問題の#2の↓や、実際の高校入試の#3↓↓にチャレンジしてみてください。

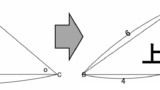
初級：裏返しの相似

　ここはまだ二等辺三角形は隠れていません。その前段階の問題です。ここは難なくクリアしたいところです。

イメージ

解

$\triangle\mathrm{BAP}\unicode[sans-serif]{x223D}\triangle\mathrm{BCA}$ より、

\begin{eqnarray}
\mathrm{BA}:\mathrm{BC} &=& \mathrm{BP}:\mathrm{BA}\\
6:\mathrm{BC} &=& 4:6\\
\therefore\; \mathrm{BC} &=& 9
\end{eqnarray}

解説

裏返しの相似で求まる感覚を持つ

$\triangle\mathrm{BAP}\unicode[sans-serif]{x223D}\triangle\mathrm{BCA}$ から、

$$\mathrm{BA}:\mathrm{BC}=\mathrm{BP}:\mathrm{BA}=\mathrm{AP}:\mathrm{CA}$$

より式\eqref{p4222eq1}, \eqref{p4222eq2}が成り立ちます。
この図のような場合に裏返しの相似から容易に”？”部分が求まる感覚を持つようにしましょう。

直角三角形の相似とも関連して理解する

　直角三角形の相似はこの裏返しの相似の特殊な形です。直角三角形の場合はさらに、方べきの定理を発想する(↓記事)こともできます。

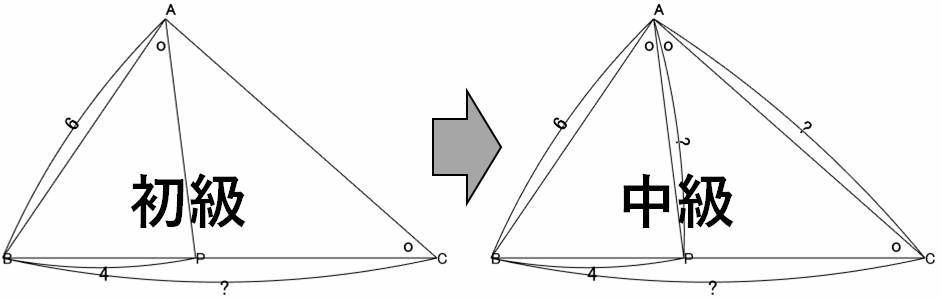
中級：角の二等分線が加わる

　辺 $\mathrm{BC}$ は初級の問題そのものです。辺 $\mathrm{AP}$, $\mathrm{AC}$ がこの問題に加わわった形です。まず辺 $\mathrm{BC}$ は難なく求めた上で、二等辺三角形が隠れている発想を持ち出せるか、です。

イメージ

解

$\triangle\mathrm{BAP}\unicode[sans-serif]{x223D}\triangle\mathrm{BCA}$ より、

\begin{eqnarray}
\mathrm{BA}:\mathrm{BC} &=& \mathrm{BP}:\mathrm{BA}\\
6:\mathrm{BC} &=& 4:6\\
\therefore\; \mathrm{BC} &=& 9
\end{eqnarray}

\begin{eqnarray}
\therefore\;\mathrm{PC} &=& \mathrm{BC}-\mathrm{BP}\\
&=& 5
\end{eqnarray}

ここで、

$$\angle\mathrm{ACP}=\angle\mathrm{CAP}$$

より、

$$\mathrm{AP}=\mathrm{PC}=5$$

$\mathrm{AP}$ は $\angle\mathrm{A}$ の二等分線なので、

\begin{eqnarray}
\mathrm{AB}:\mathrm{AC} &=& \mathrm{BP}:\mathrm{PC}\\
6:\mathrm{AC} &=& 4:5\\
\therefore\;\mathrm{AC} &=& \frac{6\times 5}{4}\\
&=& \frac{15}{2}
\end{eqnarray}

解説

初級の問題よりも条件が加わっているため、定まる部分が増えています。すなわち、角の二等分の条件が加わったことにより、この問題には3つの重要な発想が含まれていました。それは、

• $\angle\mathrm{BAP}=\angle\mathrm{BCA}$ からくる相似
• $\angle\mathrm{ACP}=\angle\mathrm{CAP}$ からくる二等辺三角形
• $\angle\mathrm{A}$ の二等分線からくる線分比

です。そのうち、二等辺三角形が意外に気づかないため、

を意識してみましょう。

まとめ

　裏返しの相似の発想を初級と位置づけ、そこに角の二等分の条件が加わることで相似の発想に加えて合計3つの発想を用いるため中級と位置づけました。

角の二等分では、この問題のように二等辺三角形が隠れているケースが多く、見逃しがちのため、それを意識できると発想力が上がります。

おススメ内部リンク記事

関連おススメ