【台形型相似の応用】入試問題実践編　辺の長さから面積比へ

問題1：22年 帝塚山学院泉ヶ丘

(1) $\mathrm{EG}:\mathrm{GF}$ を求めよ。

イメージ

　比例で内分していくイメージを持てば、目の子で長さは求められます。

この記事↓の「直接に目の子で捉える」も参照ください。

解. $\mathrm{EG}:\mathrm{GF}$ を求めよ。

(2) $\triangle\mathrm{CHF}$ と台形 $\mathrm{BCGE}$ の面積比を求めよ。

イメージ

(1)より $\mathrm{EG}:\mathrm{GF}=3:\displaystyle\frac{6}{5}$ ですが、その $\mathrm{GF}$ が成長して $\mathrm{CH}$ になるイメージを持てると見通しがよいです。

解. $\triangle\mathrm{CHF}$ と台形 $\mathrm{BCGE}$ の面積比を求めよ。

$\triangle\mathrm{AGF}\unicode[sans-serif]{x223D}\triangle\mathrm{ACH}$ で相似比が $3:5$ であるから、

$$\begin{eqnarray} \mathrm{GF}:\mathrm{CH} &=& 3:5\\ &=& \frac{6}{5}:2 \end{eqnarray}$$

ここでの目的は

$\triangle\mathrm{CHF}$ と台形 $\mathrm{BCGE}$ の面積比を求める

ことだが、その両者は高さが同じであることに注意すると、台形 $\mathrm{BCGE}$ を2つの三角形 $\triangle\mathrm{BGE}$ と $\triangle\mathrm{GBC}$ に分割して考えることにより、

$\triangle\mathrm{CHF}$ と台形 $\mathrm{BCGE}$ の面積比

は、その底辺の長さの比となることから、

$$\begin{eqnarray} \mathrm{CH}&:&(\mathrm{EG}+\mathrm{BC})\\ \displaystyle\frac{10}{5}&:&(3+5)\\ \therefore\; 1&:&4 \end{eqnarray}$$

となる。

(3) $\mathrm{EJ}:\mathrm{JD}$ を求めよ。

イメージ

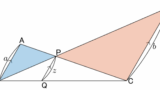
蝶々型三角形が見えれば何の問題もなく解けます。

蝶々型三角形の復習はこちら↓。

解. $\mathrm{EJ}:\mathrm{JD}$ を求めよ。

$$\begin{eqnarray} \triangle\mathrm{JEF}&\unicode[sans-serif]{x223D}&\triangle\mathrm{JDA}\\ \mathrm{EF}:\mathrm{DA}&=&\left(3+\frac{6}{5}\right):3\\ &=& \frac{21}{5}:3\\ &=& 7:5 \end{eqnarray}$$

より、

$$\mathrm{EJ}:\mathrm{JD}=7:5$$

(4) $\triangle\mathrm{CHF}$ と $\triangle\mathrm{AIJ}$ の面積比を求めよ。

イメージ

(4)は少し道のりが長いです。まずは一気通貫で見つつも、後に「解説」にて細かく分けながらイメージをつけていきます。

ポイントは、$\triangle\mathrm{CHF}$ と $\triangle\mathrm{AIJ}$ の面積を台形 $\mathrm{ABCD}$ の面積の比で表すことです。

一気通貫

解

$\triangle\mathrm{ADI}\unicode[sans-serif]{x223D}\triangle\mathrm{GEI}$ で $\mathrm{AD}=\mathrm{EG}$ より相似比は $1:1$。つまり、

$$\mathrm{EI}:\mathrm{ID}=1:1$$

これと、(3)で求めた

$$\mathrm{EJ}:\mathrm{JD}=7:5$$

とから、

$$\mathrm{EI}:\mathrm{IJ}:\mathrm{JD}=6:1:5$$

よって、

また、

ゆえに、

$$\begin{eqnarray} \frac{\triangle\mathrm{AIJ}}{\triangle\mathrm{CHF}} &=& \frac{\cancel{\text{台形}\mathrm{ABCD}}\times\frac{3}{8}\times\frac{3}{5}\times\frac{1}{12}}{\cancel{\text{台形}\mathrm{ABCD}}\times\frac{5}{8}\times\frac{16}{25}\times\frac{1}{4}}\\ &=& \frac{\frac{3}{\cancel{8}}\times\cancel{3}\cdot\cancel{\frac{1}{5}}\times\frac{1}{\cancel{3}}\cancel{\frac{1}{4}}}{\frac{\cancel{5}}{\cancel{8}}\times\frac{16}{\cancel{5}}\cdot\cancel{\frac{1}{5}}\times\cancel{\frac{1}{4}}}\\ &=& \frac{3}{16} \end{eqnarray}$$

解説：細かく分けながらイメージをつかむ

$\mathrm{EI}:\mathrm{IJ}:\mathrm{JD}$ を求める

(3)の問題で $\mathrm{EJ}:\mathrm{JD}$ を求めていますので、あとは $\mathrm{EI}:\mathrm{ID}$ が求まれば $\mathrm{EI}:\mathrm{IJ}:\mathrm{JD}$ は求まります。そのための蝶々型相似が見えればOKです。

$\mathrm{EI}:\mathrm{ID}=1:1$ が判明した後、ではどうやって $\mathrm{EI}:\mathrm{IJ}:\mathrm{JD}$ を求めればよいでしょうか。できれば、じっとにらんで $\mathrm{EI}:\mathrm{IJ}:\mathrm{JD}=6:1:5$ を見つけたいものです。この辺りを立式すると返って訳が分からなくなります。

$\triangle\mathrm{AIJ}$ を台形 $\mathrm{ABCD}$ の面積比で表す

このために、

• #1: $\triangle\mathrm{AIJ}$ を $\triangle\mathrm{AED}$ の面積比で表す
• #2: さらに拡大して $\triangle\mathrm{ABD}$ との面積比で表す
• #3: さらに拡大して台形 $\mathrm{ABCD}$ の面積まで持っていく
• #4: $\triangle\mathrm{AIJ}$ を台形 $\mathrm{ABCD}$ の面積比で表せた

まであります。

#1: $\triangle\mathrm{AIJ}$ を $\triangle\mathrm{AED}$ の面積比で表す

$\triangle\mathrm{AIJ}$ と $\triangle\mathrm{AED}$ は高さが同じなので面積比は底辺比です。

$$\begin{eqnarray} \triangle\mathrm{AIJ} &=& \triangle\mathrm{AED}\times\frac{1}{6+1+5}\\ &=& \triangle\mathrm{AED}\times\frac{1}{12} \end{eqnarray}$$

#2: さらに拡大して $\triangle\mathrm{ABD}$ との面積比で表す

$\triangle\mathrm{AED}$ と $\triangle\mathrm{ABD}$ は高さが同じなので面積比は底辺比です。

$$\begin{eqnarray} \triangle\mathrm{AED} &=& \triangle\mathrm{ABD}\times\frac{3}{3+2}\\ &=& \triangle\mathrm{ABD}\times\frac{3}{5} \end{eqnarray}$$

#3: さらに拡大して台形 $\mathrm{ABCD}$ の面積まで持っていく

$\triangle\mathrm{ABD}$ と $\triangle\mathrm{DBC}$ は高さが共通の三角形なので、面積比は底辺比です。

$$\begin{eqnarray} \triangle\mathrm{ABD} &=& \text{台形}\mathrm{ABCD}\times\frac{3}{3+5}\\ &=& \text{台形}\mathrm{ABCD}\times\frac{3}{8} \end{eqnarray}$$

#4: $\triangle\mathrm{AIJ}$ を台形 $\mathrm{ABCD}$ の面積比で表せた

以上より、

$$\triangle\mathrm{AIJ} = \text{台形}\mathrm{ABCD}\times\frac{3}{8}\times\frac{3}{5}\times\frac{1}{12}$$

$\triangle\mathrm{CHF}$ を台形 $\mathrm{ABCD}$ の面積比で表す

(2)よりすでに $\triangle\mathrm{CHF}$ と台形 $\mathrm{BCGE}$ の面積比は $1:4$ と分かっているので、$\triangle\mathrm{CHF}$ を台形 $\mathrm{ABCD}$ の面積比で表すためには台形 $\mathrm{BCGE}$ を台形 $\mathrm{ABCD}$ の面積比で表せればよいです。

台形 $\mathrm{BCGE}$ を台形 $\mathrm{ABCD}$ の面積比で表すため、

• #1: 台形 $\mathrm{BCGE}$ を $\triangle\mathrm{ABC}$ の面積比で表す
• #2: さらに拡大して台形 $\mathrm{ABCD}$ の面積まで持っていく

を行います。そうすることで、

• #3: $\triangle\mathrm{CHF}$ を台形 $\mathrm{ABCD}$ の面積比で

表します。

#1: 台形 $\mathrm{BCGE}$ を $\triangle\mathrm{ABC}$ の面積比で表す

$\triangle\mathrm{ABC}\unicode[sans-serif]{x223D}\triangle\mathrm{AEG}$ で相似比が $3:5$ なので、

$\triangle\mathrm{AEG}$ の面積は $\triangle\mathrm{ABC}$ の面積の $\displaystyle\left(\frac{3}{5}\right)^2$ 倍

です。面積比は相似比の2乗です。

従って、

$$\begin{eqnarray} \text{台形}\mathrm{BCGE} &=& \triangle\mathrm{ABC}-\triangle\mathrm{AEG}\\ &=& \triangle\mathrm{ABC} – \triangle\mathrm{ABC}\times\left(\frac{3}{5}\right)^2\\ &=& \triangle\mathrm{ABC}\left(1-\frac{9}{25}\right) \end{eqnarray}$$

です。

#2: さらに拡大して台形 $\mathrm{ABCD}$ の面積まで持っていく

$\triangle\mathrm{ABC}$ と $\triangle\mathrm{ADC}$ は高さが共通の三角形なので、面積比は底辺比です。

$$\begin{eqnarray} \triangle\mathrm{ABC} &=& \text{台形}\mathrm{ABCD}\times\frac{5}{3+5}\\ &=& \text{台形}\mathrm{ABCD}\times\frac{5}{8} \end{eqnarray}$$

#3: $\triangle\mathrm{CHF}$ を台形 $\mathrm{ABCD}$ の面積比で表せた

以上より、

$$\triangle\mathrm{CHF} = \text{台形}\mathrm{ABCD}\times\frac{5}{8}\times\left(1-\frac{9}{25}\right)\times\frac{1}{4}$$

いよいよ $\triangle\mathrm{CHF}$ と $\triangle\mathrm{AIJ}$ の面積比を求める

$$\begin{eqnarray} \triangle\mathrm{AIJ} &=& \text{台形}\mathrm{ABCD}\times\frac{3}{8}\times\frac{3}{5}\times\frac{1}{12}\\ \triangle\mathrm{CHF} &=& \text{台形}\mathrm{ABCD}\times\frac{5}{8}\times\left(1-\frac{9}{25}\right)\times\frac{1}{4} \end{eqnarray}$$

より、

$$\begin{eqnarray} \frac{\triangle\mathrm{AIJ}}{\triangle\mathrm{CHF}} &=& \frac{\cancel{\text{台形}\mathrm{ABCD}}\times\frac{3}{8}\times\frac{3}{5}\times\frac{1}{12}}{\cancel{\text{台形}\mathrm{ABCD}}\times\frac{5}{8}\times\frac{16}{25}\times\frac{1}{4}}\\ &=& \frac{\frac{3}{\cancel{8}}\times\cancel{3}\cdot\cancel{\frac{1}{5}}\times\frac{1}{\cancel{3}}\cancel{\frac{1}{4}}}{\frac{\cancel{5}}{\cancel{8}}\times\frac{16}{\cancel{5}}\cdot\cancel{\frac{1}{5}}\times\cancel{\frac{1}{4}}}\\ &=& \frac{3}{16} \end{eqnarray}$$

まとめ

　台形型相似を中心に据えた入試問題を持ってきました。台形型相似で辺の長さを求め、その上で面積比を求める、というのが定番です。