サムネ画像のような問題を考えるとき、一般には解答1,2に示したように補助線を入れた上で三角形の相似で考えます。しかし、解答3のように線形に増えるイメージで捉えることができれば、至極簡単に暗算で答えを出せるようになります。
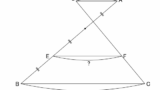
ねじれても考え方は同様です↓。
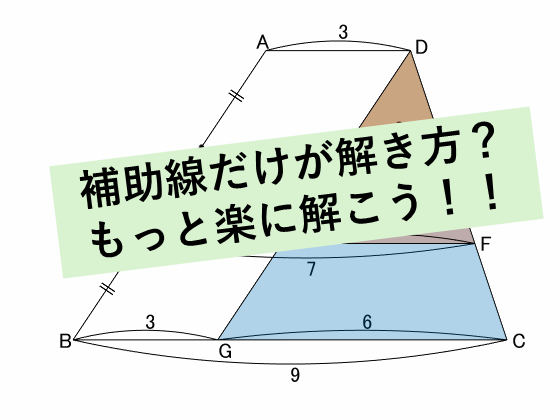
問題設定：台形の基本形
？の長さを求めよ。
解答1. $\mathrm{D}$ から $\mathrm{AB}$ に平行な補助線
イメージ
解
$\mathrm{D}$ から $\mathrm{AB}$ に平行な補助線を引き、$\mathrm{BF}$, $\mathrm{EF}$ との交点をそれぞれ $\mathrm{G}$, $\mathrm{H}$ と置くと、
\begin{eqnarray}
\mathrm{BG} &=& 3\\
\mathrm{EH} &=& 3
\end{eqnarray}
である。$$\mathrm{BG}=3$$
なので、
$$\mathrm{GC}=6$$
である。
次に、$\triangle\mathrm{DGC}\unicode[sans-serif]{x223D}\triangle\mathrm{DHF}$ で相似比が $3:2$、$\mathrm{GC}=6$ であるから、
$\mathrm{HF} = 4\quad$$(\rightarrow\text{解説1})$
であり、$\mathrm{EH}=3$ なので、
$$\mathrm{EF}=7$$
解説1. $\mathrm{HF}=4$ は目の子で求めよう
もちろん相似の比例式を立てて求めてもよいのですが、目の子で解けるようになった方が楽ですし、計算ミスもしづらいです。比例式を立てる場合は、
$$6:\mathrm{HF}=3:2$$
です。目の子で解くとは、下図のように $6$ を三等分して $2$, $4$, $6$ と増えていくイメージです。
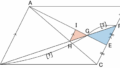
解答2. $\mathrm{A}$ から $\mathrm{C}$ への補助線
イメージ
解
$\mathrm{A}$ から $\mathrm{C}$ へ補助線を引き、$\mathrm{EF}$ との交点を $\mathrm{H}$ と置く。
$\triangle\mathrm{ABC}\unicode[sans-serif]{x223D}\triangle\mathrm{AEH}$ で相似比が $3:2$、$\mathrm{BC}=9$ であるから、
$$\mathrm{EH}=6$$
である。
同様に $\triangle\mathrm{CAD}\unicode[sans-serif]{x223D}\triangle\mathrm{CHF}$ で相似比が $3:1$、$\mathrm{AD}=3$ であるから、
$$\mathrm{HF}=1$$
である。
ゆえに、
$$\mathrm{EF}=7$$
解答3. 直接に目の子で捉える
これまで三角形の相似を用いて長さを求めてきましたが、しょせん四角形 $\mathrm{ABCD}$ は台形なので、つまり、$\mathrm{AB}$ も $\mathrm{DC}$ も線形(直線の形)なので、$\mathrm{AD}$ が平行に移動する分にはその長さは線形で(直線的に一定の割合で)変化します。
つまり、$\mathrm{EF}$ の長さは $\mathrm{AD}$ 時代の $3$ から徐々に成長して $\mathrm{BC}$ 時代に行く途中にある、というイメージです。次のようです。
このイメージを持てば、目の子で
$$\mathrm{EF} = 7$$
が求められます。
この気持ちを持って、先の解説1の「目の子で」解く部分をもう一度見てみてください。もう皆さん目の子で理解できるようになっていると思います。
解答4. 公式化してみる. 加重平均（内分点）
$\mathrm{EF}=\displaystyle\frac{na+mb}{m+n}$
これまでの解答は表題のように公式化することができます。この公式は必ずしも覚える必要はないですが、解答1や2のように補助線を引くことで必ず解けるということを理解するのと、今後も加重平均などが出てきた際にこの例も頭に浮かぶと点と点の知識が線でつながってそれぞれの理解がより深まって良いです。
$$\mathrm{EF}=\frac{na+mb}{m+n}$$
この式は加重平均の形になっています。加重平均とは重みを加味した平均であり、例えばテストで $3$ 点の人が $1$ 人、$9$ 点の人が $2$ 人いれば、平均点は
$$\frac{1\times 3+2\times 9}{2+1}=7$$
となります。ちなみに通常に平均点を計算したときの式は
$$\frac{3+9+9}{3}=7$$
なので、確かに人数で重みづけして平均を出していることが分かります。
まとめ
台形型の相似を扱いました。まずは相似を発見するために補助線を入れるところがポイントです。しかし一方で相似を見つけなくとも、線の長さは線形に増えていくイメージを持ちさえすれば、答えはほとんど一発で導くことができます。
結構このような単純なイメージが大事だったりするので、公式やよく言われるような解き方だけにとらわれず、本質的なイメージをつかむことを心がけてください。
コメント