積分の本質は限りなくゼロに近い横幅 dx を持つ短冊が敷き詰められていくイメージです。その本質が分かれば短冊だけでなく、円周を積分したら面積であることや、球の表面積を積分したら体積であること、またダメ押しでは再び円の面積は三角形の和であることもスッと理解できます。
なお、積分は微分の逆演算であることは↓の記事で取り上げます。
積分のイメージ
積分は細かい短冊の寄せ集め
例えば $f(x)=x^2$ を $0$ から $1$ まで積分することを例に考えます。定積分の式とその後の計算は、
$$\int_0^1 f(x)\,dx = \int_0^1 x^2\,dx = \frac{1}{3}\left[x^3\right]_0^1 = \frac{1}{3}\left(1^3-0^3\right) = \frac{1}{3}\tag{1}\label{eq1}$$
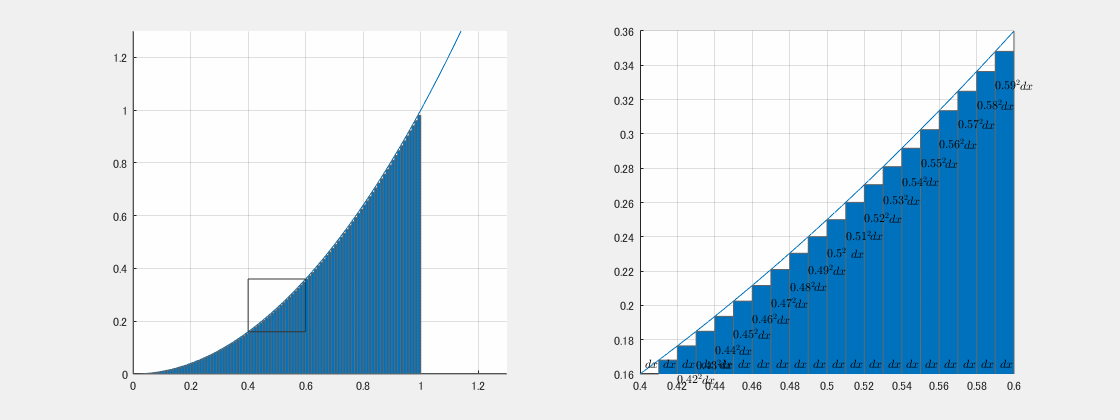
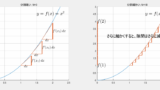
となりますが、その最初の式の意味 $\int_0^1 f(x)\,dx$ のイメージは下に示す二つの図のようです。まずは教科書的なイメージ、そして、より実践的なイメージの二つ示します。左側はマクロな視点で、そして左側にある四角の範囲だけを右側に記載してミクロな視点で見ています。
教科書的なイメージ
一つ目は、教科書的なイメージです。教科書では、短冊の幅 $h$ をどんどん小さくしていき、$\lim_{h\to 0}$ にすることで積分を表現しています。この図ではそれを表現していますが、二つ目のイメージにつなげるため、途中からなぜか幅 $h$ が $dx$ に代わっています。幅 $h$ が限りなくゼロに近づいたとき、横幅 $h$ はもはや $dx$ と書く気持ちになります。同様の気持ちは、【微分のイメージ】↓でも出てきました。
実践的なイメージ
二つ目は、より実践的なイメージです。こちらは、限りなくゼロに近い横幅 $dx$ を持つ短冊が敷き詰められていくイメージです。
この短冊の面積 $S$ は、例えば一つ一つを見ると、横幅が $dx$ で、縦の長さは場所によってもちろん異なりますが、$0.5^2$ とか $0.51^2$ とかの $x^2$ になっています。つまり、この面積の和は、
$\begin{eqnarray}
S&=&0^2dx+0.01^2dx+\cdots\\
&+&0.5^2dx+0.51^2dx+\cdots\\
&+&0.98^2dx+0.99^2dx\tag{2}\label{eq2}
\end{eqnarray}$
となるわけです。ちなみにこの場合の $dx$ は $dx=0.01$ なので、これをまじめに計算すると $S=0.3283$ になり、実際の面積 $0.33$ (式$\eqref{eq1}$)とは異なりますが近い値になっています。今は説明の便宜上 $dx=0.01$ でしたが、実際は限りなくゼロに近い横幅です。そして、この例では $f(x)=x^2$ という関数を例に取り上げたので、式$\eqref{eq2}$は次のように記載したい感じです。
$S= x^2\,dx$ を $0$ から $1$ まで足したもの
そしてこれを表現する記号が、$\int$ です。「足す」という意味の summation の頭文字 S を縦に伸ばして作った記号です。
$\tag{3}\label{eq3}$
実は短冊だけではない積分のイメージ
その1：円周を積分したら面積
円周は $2\pi r$、円の面積は $\pi r^2$ ですが、その両者は微分積分の関係にあることに気づきましたでしょうか。ここではそのイメージを、短冊イメージから発展させて理解します。それが下の図です。バウムクーヘンを作るように薄皮をくっつけていっているイメージです。図の左側に順次くっつける薄皮を、右側にその累積を示しています。
このバウムクーヘンの面積 $S$ は、その一つ一つを見ると、横幅が $dr$ で、長さは半径 $r$ のところでは $2\pi r$です。つまり、この面積の和は、
$\begin{eqnarray}
S&=&2\pi\,0\,dr+2\pi\,0.01\,dr+\cdots\\
&+&2\pi\,0.5\,dr+2\pi\,0.51\,dr+\cdots\\
&+&2\pi \,0.99\,dr\tag{4}\label{eq4}
\end{eqnarray}$
となるわけです。ちなみにこの場合の $dr$ は $dr=0.01$ なので、これをまじめに計算すると$S=3.1102$ になり、円の面積 $\pi r^2 = \pi\times 1^2=\pi$ に近くなってます。誤差は図では右側で少し白くギザギザと見える部分がありますが、その部分です。今は説明の便宜上 $dr=0.01$ でしたが、実際は限りなくゼロに近い横幅で、ギザギザも限りなくゼロに近づきます。気持ち的にはこのギザギザは求めたい青の部分に比べてすごく小さいので無視する感じです（参考：【微分のイメージ】limの気持ち）。さて、話を元に戻して、式$\eqref{eq4}$は次のように記載したい感じです。
$S= 2\pi r\,dr$ を $0$ から $1$ まで足したもの
そして、これを次のように表現します。
このまま計算を続ければ、
$$S=\int_0^1 2\pi r\,dr=\pi\left[r^2\right]_0^1=\pi$$
です。
その2：球の表面積を積分したら体積
球の表面積は $4\pi r^2$ ですが、体積は $\displaystyle\frac{4}{3}\pi r^3$ です。その両者もまた微分積分の関係にあります。先ほどはバウムクーヘンのように、あるいはコマの紐を巻き付けるように線状のものに幅を持たせて足し合わせました。今度はそれの3次元版です。りんご飴のイメージでしょうか。薄い面状のものに幅を持たせて足し合わせるイメージです。つまり、
このまま計算を続ければ、
$$V=\int_0^r 4\pi r^2\,dr=\frac{4}{3}\pi r^3$$
です。
ダメ押し：円の面積は三角形の和
積分が小さいものを寄せ集めたものであるイメージができていれば、円の面積を次のように三角形の寄せ集めイメージで計算することもできます。
左の図は上の図（動画）の左側の□部分であり、拡大図です。□があまりにも小さくて線にしか見えませんが。なお、拡大図は見やすいように縦横比は等しくなく、崩しています。
さて、青の部分の面積を求めたいのですが、それは赤の部分まで含めて考えれば三角形です。赤の底辺の長さは青の弧の長さとほぼ等しいので、$r\, d\theta$ と置けます。両者の誤差は今考えている $r\, d\theta$ に比べて非常に小さいので無視できます（参考：【微分のイメージと応用例】limの気持ち）。そうすると、赤の部分まで含めた三角形の面積 $dS$ は、底辺の長さが $r\, d\theta$ で高さが半径そのものなので $r$ ですから、
です。これを、$\theta$ が$0$から$2\pi$まで足せば円になるので、円の面積 $S$ は、
$$S=\int_0^{2\pi}\frac{1}{2}r^2\, d\theta=\frac{1}{2}r^2\int_0^{2\pi}\, d\theta=\frac{1}{2}r^2\left[\theta\right]_0^{2\pi}=\pi r^2$$
となります。注意しておいてほしいのは、ここでは $\theta$ について積分をするのであって、$\displaystyle\frac{1}{2}r^2$ は $\theta$ とは無関係の変数なので積分の外に出る、ということです。
私が小学生のときに円の面積を習った際の先生の説明が衝撃的で今でも覚えています。それは下の図のようで、まず左図のように円を小さな円弧に分けて横に並べると。そうすると、底辺の長さの合計は円周 $2\pi r$ になり、高さは全て $r$ のときんときんの三角形がたくさんできる。三角形は高さが同じなら頂点を横に移動させても面積は変わらないので、頂点を全て一か所にまとめると右図のようになる。そうすれば、三角形の面積に帰着するから、$\pi r^2$ になると。細かく分けてから足し合わせるという発想にすごく衝撃を受けました。これこそが積分の発想なのですね。
応用例：物理ではこのような考え方をよく使う
積分を習い始めたばかりの人は下記は少し難しく感じると思います。そんなもんか、くらいに読み飛ばしてもらえればよいです。一方、物理ですでに習った人はぜひ会得してほしいです。
速度を積分すると変位
速度を積分すると変位になります。逆に変位を微分すると速度になります。変位と速度とは微分積分の関係にあります。なお、微分と積分が逆の関係にあることは【微分積分学の基本定理】で詳しく述べていますので、ぜひそちらも覗いてみてください。
微小な時間の間の速度は一定：短冊を考える
ある時刻 $t$ において速度が $v(t)$ だとします。微小な時間 $dt$ の間の速度は一定と考え、この微小時間 $dt$ の間に進んだ距離 $dx$ は
$$dx=v(t)\, dt\tag{1}\label{p409eq1}$$
です。この、「微小な時間 $dt$ の間の速度は一定と考え」の部分がなんともモヤモヤするかもしれないですが、これが冒頭に説明をした、積分は細かい短冊の寄せ集めです。「細かい短冊」という部分に「微小な間は一定」という気持ちが含まれています。この細かい短冊を寄せ集めれば、つまり積分すれば、考えている範囲での進んだ距離になります。
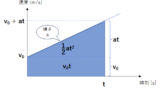
等速度運動
例えば等速度運動では左図のようです。
この場合は $v(t)$ は一定値 $v_0$ なので、グラフはこのように横一直線であり、積分をすると、
$$x=\int_0^t v(t)\, dt = \int_0^t v_0\, dt=\left[v_0\, t\right]_0^t = v_0\, t$$
となりますが、これは単に長方形の面積を求めただけです。
等加速度運動
同じように等加速度運動の場合は左図のようです。
この場合は $v(t)$ は加速度 $a$ で加速しており、速度は直線的に変化しています。積分をすると、
$$x=\int_0^t v(t)\, dt = \int_0^t (v_0+at)\, dt=\left[v_0\, t+\frac{1}{2}at^2\right]_0^t = v_0\, t+\frac{1}{2}at^2$$
となりますが、これもこの台形の面積を求めただけではあります。
等加速度運動の3公式をさらに詳しく
いずれにせよ大事なのは、決してこれらの公式を公式として暗記するのではなく、その元になる理論を理解することです。今の場合は、変位は速度に時間をかけたものであり、式$\eqref{p409eq1}$の理解です。この辺りは【等加速度運動の3公式】微分積分を用いて導出し、完全理解↓でさらに詳しく述べています。
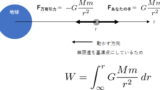
力を積分すると仕事：位置エネルギー
保存力に逆らって外力が行った仕事が位置エネルギーとして蓄えられます。例えば、万有引力による位置エネルギーでは、万有引力が
$$F_{万有引力} = -G\frac{Mm}{r^2}$$
なので、それに釣り合う力で支えている外力は、
$$F_{外力} = G\frac{Mm}{r^2}$$
です。この力で微小距離 $dr$ だけ移動させれば、その間に外力が行った仕事 $dW_{外力}$ は、
$$dW_{外力} = G\frac{Mm}{r^2}\, dr$$
です。それを無限遠$(\infty)$から $r$ の位置まで持ってきたときの外力が行った仕事の合計が位置エネルギーであり $dW_{外力}$ の短冊を足し合わせばよいので、
\begin{eqnarray}
W_{外力} &=& \int_{\infty}^{r}G\frac{Mm}{r^2}\, dr\\
&=& -GMm\left[\frac{1}{r}\right]_{\infty}^{r}\\
&=& -G\frac{Mm}{r}
\end{eqnarray}
となります。
詳しくは、【力学的エネルギー保存の法則】↓をご覧ください。
ロケットの推進
ロケットは燃料を後方に噴射することにより推進します。これは運動量保存の法則です。噴射した燃料の質量と噴射速度に応じてロケット自身の速度が増します。それを足し合わせればロケットの最終的な速度になります。【ツィオルコフスキーのロケット方程式】↓をご覧ください。
テニスボールの行方
空気抵抗とスピンがある場合のラリー軌道を求めました。運動方程式を立ててそれを解きますが、その際に時間 $dt$ を細かく区切って計算するという短冊手法を取っています。↓の「発展：シミュレーションってどうやっているの？」の節です。
まとめ
積分の本質的なイメージを理解しました。それは、細かい短冊やバウムクーヘンなどを足し合わせることです。
それにより、円の面積$(\pi r^2)$と円周$(2\pi r)$が微分積分の関係にあることなども見えてきました。また、物理ではこのような考え方をふんだんに使っていくのだな、という雰囲気を味わいました。
このイメージを持っておくことで、積分を単なる難しい計算問題ではなく、しっかりと役に立つ道具にしていくことができます。ぜひこのイメージを会得してください。
コメント