同じ直角三角形が2つで二等辺三角形。言われれば当たり前ですが、気づくのは案外難しい。角の二等分線がそれを示していたりとか(問題1)、線を延長する(かつ合同を見つける)と見えてくるとか(問題2)。
問題2は線を延長する発想が思いつかず、二等辺三角形を発見できない場合もあります。そのような場合でも強引に解くことができる場合があります(解2:中3で習う「三平方の定理」を用います)。入試では必ずしも美しく解く必要はないので、最後の手段として武器にできると強いです。
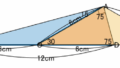
問題1. ’21 成城学園高校
?の面積を求めよ。

問題の図形には怪しげにも \angle\mathrm{B} に角の二等分線が引かれています。もちろんこれが重要な条件になります。角の二等分線を見たときの発想のコツは解説で述べます。
解1. 高さを用いる方法
イメージ
解
\triangle\mathrm{ABE}\equiv\triangle\mathrm{DBE} より、
\mathrm{BD}=\mathrm{BA}=14
すると、\mathrm{BC}=20 より、
\mathrm{DC}=6

\mathrm{AE}=\mathrm{ED} より、
\begin{eqnarray} \mathrm{EF} &=& \frac{1}{2}\mathrm{DC}\\ &=& 3 \end{eqnarray}

[ここまで解1,2で共通]\tag{★}\label{p3760-1}
\triangle\mathrm{AEF}=9 で底辺の長さ \mathrm{EF}=3 より、
高さは 6
\mathrm{AE}=\mathrm{ED} より \triangle\mathrm{EBD} の高さも 6 となるから、求める面積 \triangle\mathrm{EDB} は、
\begin{eqnarray} \triangle\mathrm{EDB} &=& \frac{1}{2}\cdot 14\cdot 6\\ &=& 42 \end{eqnarray}

解2. 面積比を用いる方法
解イメージ
解
[\eqref{p3760-1}まで同じ]
\triangle\mathrm{AEF}\unicode[sans-serif]{x223D}\triangle\mathrm{ADC} で相似比 1:2 より、面積比は 1:4。よって、
\triangle\mathrm{ADC} = 36

\triangle\mathrm{ADC} と \triangle\mathrm{ADB} は高さが共通の三角形なので、面積比は底辺の比となる。すなわち、
\begin{eqnarray} \triangle\mathrm{ADB}:\triangle\mathrm{ADC} &=& 14:6\\ \triangle\mathrm{ADB}:36=14:6\\ \therefore\;\triangle\mathrm{ADB}=84 \end{eqnarray}
求めたい \triangle\mathrm{EBD} はこれの半分なので、
\triangle\mathrm{EBD}=42

解説1. \mathrm{BD}=\mathrm{BA}=14 が見えるかがポイント
これが見えれば \triangle\mathrm{AEF}\unicode[sans-serif]{x223D}\triangle\mathrm{ADC} はすでに見えていると思うので、解1で解くにせよ、解2で解くにせよ、\triangle\mathrm{ABD} が二等辺三角形であることを発見することがポイントです。
解説2. 角の二等分線を見たときの発想法
問題の図形には怪しげにも \angle\mathrm{B} に角の二等分線が引かれていました。もちろんこれが重要な条件になりまするわけで、角の二等分線を見たら、
その先の角度(この場合は \angle\mathrm{E} )が
- 直角でなければ線分比を
- 直角なら二等辺三角形を
もう一つ別の角に同じ角度があれば
- 相似と二等辺三角形を
そして、平行線に向かって二等分線が引かれていれば、
- 二等辺三角形を
疑うのが基本の発想です。今回は直角なので二等辺三角形を疑いました。
3つ目の「相似と二等辺三角形を疑う」は↓に、
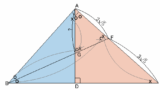
4つ目の「二等辺三角形を疑う」は↓にて詳しく扱っています。
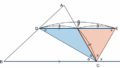
問題2. こうなるといいな、からの発想が大事かも
?の長さを求めよ。

解1. 図形問題らしい解き方
直角三角形が2つで二等辺三角形。この発想が頭にあれば、こうなっていれば↓いいな、という希望的観測が成り立ちます。すなわち、直角三角形を折り返した時、ちょうど \mathrm{EBC} が一直線になるような状況です。この希望的観測があれば、線を延長してみよう、という気になります。

解イメージ
解
線を延長する
\mathrm{CB} と \mathrm{DM} の延長線の交点を \mathrm{E} と置く。

\mathrm{DM}=\mathrm{EM} ならいいな、と思う。
ここで、\triangle\mathrm{ADM}\equiv\triangle\mathrm{BEM} を示す。
まず、問題文より \mathrm{AM}=\mathrm{BM}。

次に、\mathrm{AD}/\! /\mathrm{EC} より、
\angle\mathrm{MAD}=\angle\mathrm{MBE}。

さらに、対角の関係より、
\angle\mathrm{BME}=\angle\mathrm{AMD}。

一辺とその両端の角が等しいから、
\triangle\mathrm{ADM}\equiv\triangle\mathrm{BEM}

合同なので、\mathrm{DM}=\mathrm{EM}
\triangle\mathrm{ADM}\equiv\triangle\mathrm{BEM}
より、
\mathrm{DM}=\mathrm{EM}
また、
\mathrm{AD}=\mathrm{BE}=1

二等辺三角形を発見!
\mathrm{DM}=\mathrm{EM}
かつ
\angle\mathrm{CMD}=\angle\mathrm{CME}=90^\circ
なので、\triangle\mathrm{CDE} は二等辺三角形。

\mathrm{CD}=\mathrm{CE} より、問題解決
よって、
\begin{eqnarray} \mathrm{CD} &=& \mathrm{CE}\\ &=& 5 \end{eqnarray}
解2. 強引な解き方
図形問題的解法が思いつかないときには非常に強力な武器になりますので、この解き方も折に触れて慣れていくとよいです。これに耐えられる計算力も鍛えましょう。
解
点Cを原点に取り、点Dを (x,y) と置くと、題意より他の点は図のように置ける。

ここで、\triangle\mathrm{CDH} に三平方の定理を適用して、
\mathrm{CD}^2 = x^2+y^2\tag{1}\label{p3760eq1}
また、\triangle\mathrm{CDM} に三平方の定理を適用するため、\mathrm{DM}^2, \mathrm{MC}^2 を求める。
\begin{eqnarray} \mathrm{DM}^2 &=& \left(x-\frac{x-5}{2}\right)^2+\left(y-\frac{y}{2}\right)^2\\ &=& \left(\frac{x+5}{2}\right)^2+\left(\frac{y}{2}\right)^2\\ \mathrm{MC}^2 &=& \left(\frac{x-5}{2}\right)^2+\left(\frac{y}{2}\right)^2 \end{eqnarray}
よって、
\begin{eqnarray} \mathrm{CD}^2 &=& \mathrm{DM}^2+\mathrm{MC}^2\\ &=& \left(\frac{x+5}{2}\right)^2+\left(\frac{y}{2}\right)^2+\left(\frac{x-5}{2}\right)^2+\left(\frac{y}{2}\right)^2\\ &=& \frac{1}{4}\left((x+5)^2+(x-5)^2+y^2+y^2\right)\\ &=& \frac{1}{4}(2x^2+50+2y^2)\\ &=& \frac{1}{2}(x^2+y^2+25)\tag{2}\label{p3760eq2} \end{eqnarray}
よって、\eqref{p3760eq1}, \eqref{p3760eq2}を等しいと置いて、
\begin{gather} x^2+y^2=\frac{1}{2}(x^2+y^2+25)\\ \therefore\; x^2+y^2=25\tag{3}\label{p3760eq3} \end{gather}
求める長さ \mathrm{CD}^2 は x^2+y^2 なので\eqref{p3760eq3}より
\begin{eqnarray} \mathrm{CD}^2 &=& x^2+y^2\\ &=& 25\\ \therefore\;\mathrm{CD} &=& 5 \end{eqnarray}
解説. 解2の式\eqref{p3760eq3}について
式\eqref{p3760eq3}の意味について少し考えてみます。(x,y) は点 \mathrm{D} として条件を満たすような値ですが、それは一意には決まらずに\eqref{p3760eq3}を満たしさえすればなんでもよいと言っています。つまり、\mathrm{CD}=5 を満たすような点 \mathrm{D} なら条件を満たすような図は作れる、と主張しています。
実際、点\mathrm{D} の位置を変えた(でも、\mathrm{CD}=5 は守った)点にしても、下図のように条件を満たす図は書けます。

まとめ
二等辺三角形を発見することがミソな例題を見てきました。角の二等分線と直角三角形を見たら二等辺三角形が発見できたことになります。また、底辺の長さが等しいかつ直角三角形も二等辺三角形です。直角三角形はどうも、二等辺三角形と相性がよさそうですね。
直角三角形が二等辺三角形と相性が良い例として↓もあります。
角の二等分線から二等辺三角形を発見する例としては、直角三角形のほか、↓の記事のように平行線もあります。
このような典型例を頭に刷り込ませることにより、新しい問題にも立ち向かえる発想力が鍛えられます。そのためにぜひここのアニメーションを大いに利用してください。眺めるだけで記憶に刷り込んでいきます。


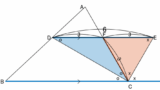
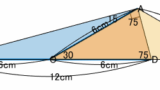
コメント