単原子分子理想気体の内部エネルギーが 3/2nRTであることを一行で示します。一行で書くことで見通しがパッと明るくなります。
このネタは2024年の共通テストでも出ました。↓の記事で取り上げています。
理解したい内容と結論
理解したい内容
理解したい内容を問題風にします。
単原子分子理想気体の内部エネルギー $U$ が
$$U=\frac{3}{2}nRT$$
であることを次の方針を参考に示せ。
方針：単原子分子理想気体では、分子の運動エネルギーの総和が内部エネルギーである。
結論
理解したい結論は下の図の上の式です。これが理解できれば
下の式の運動エネルギーの総和が内部エネルギー
であるとの等式を立てることにより、内部エネルギーが $\displaystyle\frac{3}{2}nRT$ であることが理解できます。
現段階ではもちろん訳が分からないと思いますので、次でステップバイステップで解説します。
一行の式の成り立ちを見る
まずは1つの分子で考える
図のような一辺 $L$ の立方体の中にある単原子分子理想気体の一粒を考えます。それも、まずは簡単のために $x$ 方向成分のみを考えることにします。
1回当たりの力積は $ 2mv_x$
分子の運動量は壁に衝突する前 $mv_x$ であったものが $-mv_x$ に変化したため、運動量の変化量 $\Delta p_1$ は
$$\Delta p_1=(-mv_x)-(mv_x)=-2mv_x$$
です。作用反作用の法則より、壁は同じだけの力積を分子から受けるので、その力積 $\Delta p_2$ は
$$\Delta p_2 = 2mv_x$$
です。
結論の図式に書いてある
1回当たりの力積
は、正確には「分子が壁に与える」1回当たりの力積です。
力積については↓の記事でも少し説明をしていますので、見てみてください。
1秒当たりの回数は $\displaystyle\frac{v_x}{2L}$
分子の速さは $v_x$ なので1秒間に $v_x$ 進みます。そして箱を往復する $2L$ だけ進むと再び今注目している壁に衝突します。
従って1秒間に分子は（今注目している）壁に
$\displaystyle\frac{v_x}{2L}$ 回
衝突します。
すると、1回当たりには $2mv_x$ だけの力積を壁に与えるので、両者の積
$$2mv_x\times\frac{v_x}{2L}$$
は1秒あたりに壁に与える力積です。
1秒当たりの力積とはすなわち力である
そしてここで注意するのは、1秒間当たりの力積とは力そのものであるということです。$\Delta t=1$ だからです。従ってこの値は
分子1個が壁に与える力
そのものを表します。つまり、
$$f=2mv_x\times\frac{v_x}{2L}$$
です。
箱の中の分子 $nN_A$ 個が総出で壁を押す
箱の中には $nN_A$ 個の分子が入っています。これまで断っていなかったですが、
- $n$：モル数
- $N_A$：アボガドロ数
です。従って両者の積 $nN_A$ は箱の中にある分子の総数です。
先ほどの力 $f$ で分子 $nN_A$ 個が押すので、
\begin{eqnarray}
F &=& f\, nN_A\\
&=& 2mv_x\times\frac{v_x}{2L}\times nN_A
\end{eqnarray}
が、
箱の中の全部の分子によって壁を押す力
を表します。
力を面積で割ると圧力
壁の面積は $L^2$ なので、先ほど求めた力をこの面積で割れば圧力です。
\begin{eqnarray}
P &=& \frac{F}{L^2}\\
&=& 2mv_x\times\frac{v_x}{2L}\times nN_A\times\frac{1}{L^2}
\end{eqnarray}
体積を掛けると状態方程式
箱の体積は $L^3$ です。これを掛けると状態方程式である
$$PV=nRT$$
が成り立ちます。この方程式は理想気体で成り立ちます。
従って先ほど求めた $P$ に体積 $L^3$ を掛け、それが $nRT$ に等しいと置きます。
\begin{eqnarray}
PV &=& 2mv_x\times\frac{v_x}{2L}\times nN_A\times\frac{1}{L^2}\times L^3\\
&=& nRT\tag{1}\label{p3452eq1}
\end{eqnarray}
上の式が導けた
以上より、上側の式が導けました。
運動エネルギーの総和が内部エネルギー
左辺を整理しておく
今後の式変形のために左辺を式変形しておきます。
\begin{eqnarray}
&&\cancel{2}mv_x\times\frac{v_x}{\cancel{2}\cancel{L}}\times nN_A\times\frac{1}{\cancel{L^2}}\times\cancel{L^3}\\
&&\quad = m\, v_x^2\, n\, N_A\tag{2}\label{p3452eq2}
\end{eqnarray}
$v_x$ を $v$ に置き換える
箱の中の気体は全体としては静止している（箱は動いていない）ので、
$$\overline{v_x^2}=\overline{v_y^2}=\overline{v_z^2}$$
です。$\overline{\quad}$ は平均を意味します。分子の速度は個々バラバラですが、平均をとれば同じだ、ということです。そしてさらに、
$$\overline{v_x^2}+\overline{v_y^2}+\overline{v_z^2}=\overline{v^2}$$
なので結局、
$$\overline{v_x^2}=\overline{v_y^2}=\overline{v_z^2}=\frac{1}{3}\overline{v^2}$$
です。
左辺の $v_x$ を $v$ で置き換える
これを用いて式\eqref{p3452eq2}の $v_x$ を $v$ に書き換えます。その際、平均をとることにします。
\begin{eqnarray}
&&\cancel{2}mv_x\times\frac{v_x}{\cancel{2}\cancel{L}}\times nN_A\times\frac{1}{\cancel{L^2}}\times\cancel{L^3}\\
&&\quad = m\, \overline{v_x^2}\, n\, N_A\\
&&\quad = \frac{1}{3}\,m\overline{v^2}\,nN_A\tag{3}\label{p3452eq3}
\end{eqnarray}
運動エネルギーを表に出す
運動エネルギーは
$$\frac{1}{2}m\overline{v^2}$$
なので、これを表に出すように式変形します。すなわち式\eqref{p3452eq3}は
\begin{eqnarray}
&&\cancel{2}mv_x\times\frac{v_x}{\cancel{2}\cancel{L}}\times nN_A\times\frac{1}{\cancel{L^2}}\times\cancel{L^3}\\
&&\quad = \frac{1}{3}\,m\overline{v^2}\,nN_A\\
&&\quad = \frac{2}{3}\times\frac{1}{2}m\overline{v^2}\times nN_A
\end{eqnarray}
となるので、式\eqref{p3452eq1}に戻すと、
\begin{eqnarray}
PV &=& 2mv_x\times\frac{v_x}{2L}\times nN_A\times\frac{1}{L^2}\times L^3\\
&=& \frac{2}{3}\times\frac{1}{2}m\overline{v^2}\times nN_A\\
&=& nRT
\end{eqnarray}
すなわち、
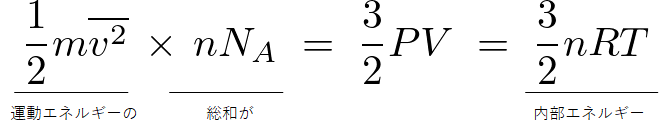
が得られました。
単原子分子理想気体でない場合はどうなるのか？
単原子分子理想気体という言葉には二つの条件が含まれています。
- 単原子分子
- 理想気体
です。
単原子分子
文字通り一つの原子のみから成る分子です。ヘリウムやアルゴンなどの希ガスがそれにあたります。窒素や酸素などは O$_2$, N$_2$ と2原子分子であり、単原子分子ではありません。
単原子分子でない場合、分子の内部エネルギーには分子の回転や振動などのエネルギーも含まれ、複雑です。
それを分かりやすく説明しているページがないかと探したところ、信州大学のとある研究室のページに分かりやすいものがありました。そこでは「自由度」という表現で表が書かれていましたが、それを上記で求めた $\displaystyle\frac{3}{2}R$ （これは実は定積モル比熱です）の表現に書き直して、そしてそのページの後半の記述も取り入れて書き換えて記載してみます。
| 常温 | 高温 | |||
|---|---|---|---|---|
| 並進 | 回転 | 振動 | ||
| 単原子分子 | ||||
| 2原子分子 | ||||
| 3原子分子(直線型) | ||||
| 3原子分子(非直線型) | ||||
これは、2原子分子の場合、常温では並進のエネルギーに加えて回転のエネルギーも加わるため定積モル比熱は $\displaystyle\frac{5}{2}R$ となり、さらに高温になると振動のエネルギーも加わり定積モル比熱は $\displaystyle\frac{7}{2}R$ となることを言っています。
しかし、大学受験で出てくるのはおそらく単原子分子までだと思いますので、ここは素直に
単原子分子だけでよかった
と胸をなでおろし、定積モル比熱が $\displaystyle\frac{3}{2}R$ であることだけ記憶にとどめておきましょう。
理想気体
分子間の相互作用が無い状態を指します。平たく言うと、ぶつからないということです。つまり、分子密度が小さい（希薄）ということです。通常我々が暮らしている空気では、体積比で1/1000くらいの密度ですので十分に希薄です。
まとめ
単原子分子理想気体では、分子の運動エネルギーの総和が内部エネルギーであることを用いて、内部エネルギー $U$ が
$$U=\frac{3}{2}nRT$$
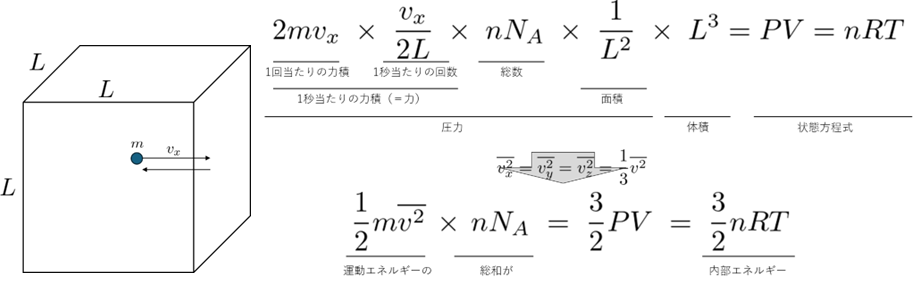
であることを導きました。その導出は次の図に集約されます。
この式一行を自分で書けるようになれば、高校範囲の気体分子運動論の大部分は理解できたと言えます。
コメント