三平方の定理とは直角三角形の3辺に成り立つ式で次のようなものです。
$a^2+b^2=c^2$
三平方の定理の証明は複数ありますが、ここでは図形を用いた証明と数式を用いた証明を紹介します。証明問題そのものが入試で出ることは稀ですが、なかなか美しいので一度経験しておくのもよいでしょう。
なお、三平方の定理の拡張として↓の余弦定理があります。（高校範囲です）
図形を用いた証明：小学生にも理解ができ、また手品のようで美しい
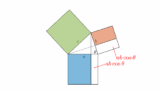
証明の方針は、図の青の面積と赤の面積の和が緑の面積になる、というものです。面積を等しいままに変形していく様は手品を見ているようです。
証明の方針：
青の面積($a^2$)と
赤の面積($b^2$)の和が
緑の面積($c^2$)
証明動画
一気通貫で眺めます。アニメーションです。再生ボタンを押してください。
ステップ・バイ・ステップ解説
高さが変わらなければ三角形の面積は等しい
辺$\mathrm{AD}/\! /$辺$\mathrm{CB}$ なので、$\triangle\mathrm{ADB}$ の面積と $\triangle\mathrm{ADC}$ の面積は等しいです。
回転させても面積は等しい
$\triangle\mathrm{ADC}$ を回転させたものが$\triangle\mathrm{ABI}$ です。
再び、高さが変わらなければ三角形の面積は等しい
今度は 辺$\mathrm{AI}/\! /$辺$\mathrm{BJ}$ です。従って、$\triangle\mathrm{AIB}$ の面積と$\triangle\mathrm{AIJ}$ の面積は等しいです。
対角線は長方形の面積を半分に分ける
もう半分側も面積は同じです。
赤も同様
同様に考えられますので、完成の絵だけ載せて省略します。
数式を用いた証明：中学生以上なら実はこちらの方が圧倒的に単純
実際に証明をするならこちらの方が圧倒的に単純です。証明の方針は、同じ面積を別の見方で表現する、です。
証明の方針：同じ面積を別の見方で表現する。
同じ面積を別の見方で表現
下記のように別の見方をします。
左側の面積
左側に注目すると、一辺の長さが $a+b$ の正方形なので、その面積は $(a+b)^2$ です。展開しておくと、
$$a^2+2ab+b^2$$
です。
右側の面積
右側に注目すると、真ん中の正方形(面積:$c^2$)と端の4つの直角三角形(面積:$\displaystyle\frac{1}{2}ab\times 4$)から成ります。従ってその面積は、
$$c^2+2ab$$
左側の面積と右側の面積は等しい
両者を等しいと置くことにより、
\begin{eqnarray}
a^2+2ab+b^2&=&c^2+2ab\\
\therefore\; a^2+b^2&=&c^2
\end{eqnarray}
まとめ
三平方の定理の証明を行いました。証明自体が入試に出ることは稀ですが、三平方の定理を利用する問題は必ずと言ってよいほど入試に出ます。証明を知ることはその定理を使う上での自信になりますので、このように経験しておくとよいと思います。
コメント