【積の微分公式】微分が互い違いに出てくる理由を展開公式で理解。証明も。

　積の微分公式は出てきます。その理由をします。結論を先に示すと、これは展開公式である $(a+b)(c+d)=ac+ad+bc+bd$ の $ad+bc$ に当たります。その辺りをじっくりと見ていきます。後半ではちゃんとした証明もしていきます。

　近しい謎公式に↓があると思います。この記事の後にでもどうぞ。

【合成関数の微分】かっこのままで微分微分が連鎖するイメージをアニメーションで理解

ここでの目的は、y=(2x-1)^2やy=sin(x)^2といった合成関数を楽に微分することです。かっこのままで微分できるようになります。そのため、微分が連鎖するイメージをしっかりと会得します。

公式の確認と理解したい結論
- 公式の確認：微分が互い違いに出てくる
- 理解したい結論：微分の互い違いは展開公式の $ad+bc$ である！
理解のための具体例
- まずは具体的に考えてみる
- 証明につなげるために抽象的に考えなおす
定義式からしっかりと証明
- いよいよ定義式から証明する
まとめ

公式の確認と理解したい結論

公式の確認：微分が互い違いに出てくる

　確かに、積の微分公式は次のとおりであり微分が互い違いに出てきています。

$(f(x)g(x))^{\prime} = f^{\prime}(x)g(x)+f(x)g^{\prime}(x)$

その理由の結論を先に示すと、これは展開公式である

$(a+b)(c+d) = ac+ad+bc+bd$

の

$ad+bc$

の部分に当たります。

理解したい結論：微分の互い違いは展開公式の $ad+bc$ である！

　結論は下の式に集約されています。この式から「なるほどね、確かに $ad+bc$ だわ」と理解できればこの記事の目的は達成です。

$\begin{eqnarray} dy&=&\left(f(x)+df(x)\right)\left(g(x)+dg(x)\right)\\ &&-f(x)\,g(x) \end{eqnarray}$

それを理解するために具体例として

$dy=(1+0.01)(1+0.02)-1\times 1$

を次の章で納得していきます。

理解のための具体例

　ここでは具体例として下記を考えます。

$f(x)=x$
$g(x)=x^2$

　この積は

$h(x)=f(x)g(x)=x^3$

なので、積の微分公式を使うまでもなくその微分は

$h^{\prime}(x)=3x^2$

なのですが、それをここではあえて分けて考えます。

まずは具体的に考えてみる

　さらに具体的に $x=1$ の近辺で考えます。です（【微分のイメージ】dy/dxは分数であり、傾きを表している気持ち）。下図の動画ではその $dy$ が

$dy=(1+0.01)(1+0.02)-1\times 1$

であると求められています。この辺りですでに展開公式っぽい感じがしませんか？。

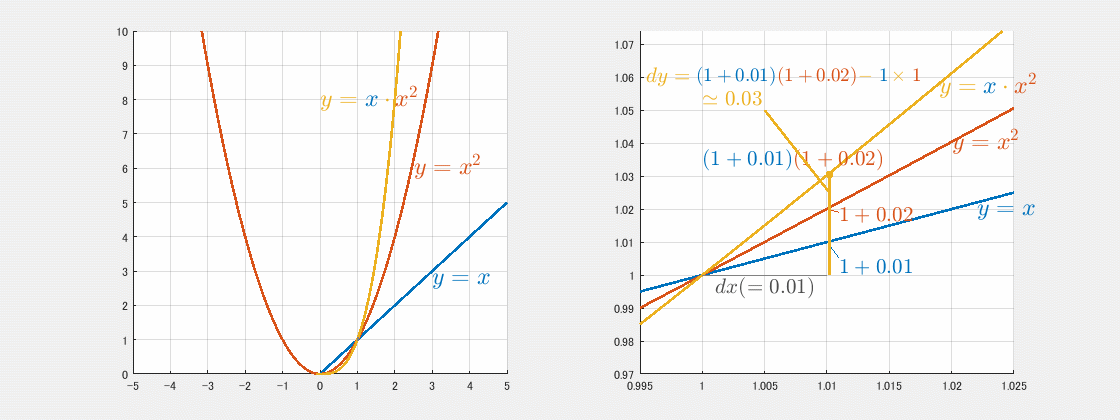
左図も右図も $y=x$ と、そしてその積のを書いていますが、右図は $x=1$ 付近の超拡大です。超拡大図では曲線も直線のように見えます。 $x=1$ 付近で超拡大したのでであり、であることに注意すると、微小距離 $dx=0.01$ だけ進んだところでのそれぞれの $y$ の値は、

$x=1$ から $dx=0.01$ 進んだ青のグラフの $y$ の値は $1+0.01$
$x=1$ から $dx=0.01$ 進んだ赤のグラフの $y$ の値は $1+0.02$

となります。

従ってその積である黄は、

$x=1$ から $dx=0.01$ 進んだ黄のグラフの $y$ の値は両者の積なので
$(1+0.01)$ $(1+0.02)$

です。

もともとの $y$ の値は青が $1$ 、赤も $1$ なので、

$x=1$ での青のグラフの $y$ の値と赤のグラフの $y$ の値との積は、 $\times$ $1$

です。すると黄色の増分である $dy$ は、

$=($ $)($ $)-$ $\times$ $1$

と表現できます。

展開して計算を進めると、

$\begin{eqnarray} dy&=&(1+0.01)(1+0.02)-1\\ &=&(\cancel{1}+0.03+0.01\times 0.02)-\cancel{1}\\ &=&0.03+0.01\times0.02\\ &\simeq& 0.03 \end{eqnarray}$

となります。

この計算の中に展開公式が出てきました。ここで、します。ここの感覚が難しいかもしれません。ここの感覚については、【微分のイメージ】limの気持ちを参照してみてください。これで $dy$ が求められました。 $dx=0.01$ だったので、

$\displaystyle\frac{dy}{dx}=\displaystyle\frac{0.03}{0.01}=3$

となり、確かに $h(x)=x^3$ の $x=1$ での微分係数と一致します。しかし、これらの計算をしても、だから何？というモヤモヤが生じているかもしれません。まだ積の微分公式の形が見えてこないからです。次の抽象的編でそれが見えてきます。

証明につなげるために抽象的に考えなおす

　先ほどと同じ例を抽象化します。 $x=1$ や $dx=0.01$ をそのまま $x$ や $dx$ と書くことにします。そして、微小距離 $dx$ だけ進んだ時の $f(x)$ , $g(x)$ の変化量をそれぞれ $df(x)$ , $dg(x)$ と書くことにします。すると $dy$ は、

$= ($ $)($ $)-$ $f(x)$ $g(x)$

と表現できます。先ほどの具体例では

$=($ $)($ $)-$ $\times$ $1$

です。展開して計算を進めると、

$\begin{eqnarray} dy&=&\left(f(x)+df(x)\right)\left(g(x)+dg(x)\right)-f(x)\,g(x)\\ &=&\left(\cancel{f(x)\,g(x)}+df(x)\,g(x)+f(x)\,dg(x)+df(x)\,dg(x)\right)\\ &&-\cancel{f(x)\,g(x)}\\ &=&df(x)\,g(x)+f(x)\,dg(x)+df(x)\,dg(x) \end{eqnarray}$

となります。先ほどの具体例では

$\begin{eqnarray} dy &=& (1+0.01)(1+0.02)-1\times 1\\ &=& (\cancel{1\times 1}+0.01\times 1+1\times 0.02+0.01\times 0.02)\\ &&-\cancel{1\times 1}\\ &=& 0.01\times 1+1\times 0.02+0.01\times 0.02 \end{eqnarray}$

です。ここで、 $df(x)\,g(x)$ や $f(x)\,dg(x)$ に対してです。確かに先ほどの具体例編では、 $df(x)\,dg(x)$ は $0.01\times 0.02=0.0002$ であり、 $df(x)\,g(x)$ や $f(x)\,dg(x)$ はそれぞれ $0.01\times 1$ と $1\times 0.02$ なので、これらに比べると無視できるほど小さいです。

よって、 $df(x)\,dg(x)$ を無視すると、

$dy\simeq df(x)\,g(x)+f(x)\,dg(x)$

となりました。。 $x$ の増加量は $dx$ としているので、

$\begin{eqnarray} \frac{dy}{dx}&=&\frac{df(x)}{dx}g(x)+f(x)\frac{dg(x)}{dx}\\ &=&f^{\prime}(x)\,g(x)+f(x)\,g^{\prime}(x) \end{eqnarray}$

となり、積の微分公式が見えました。

定義式からしっかりと証明

いよいよ定義式から証明する

　最後に、微分の定義式を用いて証明します。このとき、 $0$ を足すという見事な技を使います。足す $0$ とは、

$f(x+h)\,g(x)-f(x+h)\,g(x)$

です。

$\begin{eqnarray} \left(f(x)\,g(x)\right)^{\prime}&=&\lim_{h\to 0}\frac{f(x+h)\,g(x+h)-f(x)\,g(x)}{h}\\ &=&\lim_{h\to 0}\frac{f(x+h)\,g(x)-f(x)\,g(x)+f(x+h)\,g(x+h)-f(x+h)\,g(x)}{h}\\ &=&\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\,g(x)+\lim_{h\to 0}\frac{g(x+h)-g(x)}{h}\,f(x+h)\\ &=&f^{\prime}(x)\,g(x)+f(x)\,g^{\prime}(x) \end{eqnarray}$

まとめ

　積の展開公式を展開公式から理解しました。それは、

$\begin{eqnarray} dy&=&\left(f(x)+df(x)\right)\left(g(x)+dg(x)\right)\\ &&-f(x)\,g(x) \end{eqnarray}$

を展開し、 $df(x)\, dg(x)$ を無視することで得られました。

証明も行いました。 $f(x+h)\,g(x)-f(x+h)\,g(x)$ という $0$ を足すことで微分が2つに分けられ、証明ができました。

積の微分公式は微分が互い違いに出てきて、なぜだろう、とモヤモヤしていた方も、展開公式をイメージし、腹落ちして計算を進めることができるようになっていただければ幸いです。