ここでの目的は、
- $y=(2x-1)^2$ や
- $y=\sin^2 x$
といった合成関数を楽に微分することです。特に、例1：$y=(2x-1)^2$ の微分ではかっこのままで微分できるようになります。そして、それがなぜそのようになるのかをアニメーションで理解できます。
ここの記事が理解できれば、これの逆を行くことでかっこのままで積分ができるようになります。
また、これと近しい謎公式に↓があると思います。この記事の後にでもどうぞ。
合成関数の微分のイメージ
$x$ の係数が 1 の場合：平行移動をイメージ
$y=(x-1)^2$ の微分
$y=(x-1)^2$ は、$y=x^2$ を右に $1$ だけ平行移動したグラフです（下図最左）。つまり、$y=(x-1)^2$ の微分は、$y=x^2$ の微分である $y^{\prime}=2x$ を右に $1$ だけ平行移動すればよく、
$$y^{\prime}=2(x-1)$$
となります。
$x$ の係数が1でない場合：微分が連鎖するイメージを動画で理解
この場合でも式変形により $x$ の係数を $1$ にすることができるため、上述の方法が使えます。しかしここではもう少し一般的に考えます。
$$y=(2x-1)^2$$
を微分することを例に考えます。微分とは、$\displaystyle\frac{dy}{dx}$ を求めることであり、つまり、
$x$ が微小幅 $dx$ だけ増えるとき、
$y$ が増える量 $dy$ はどれだけなのか
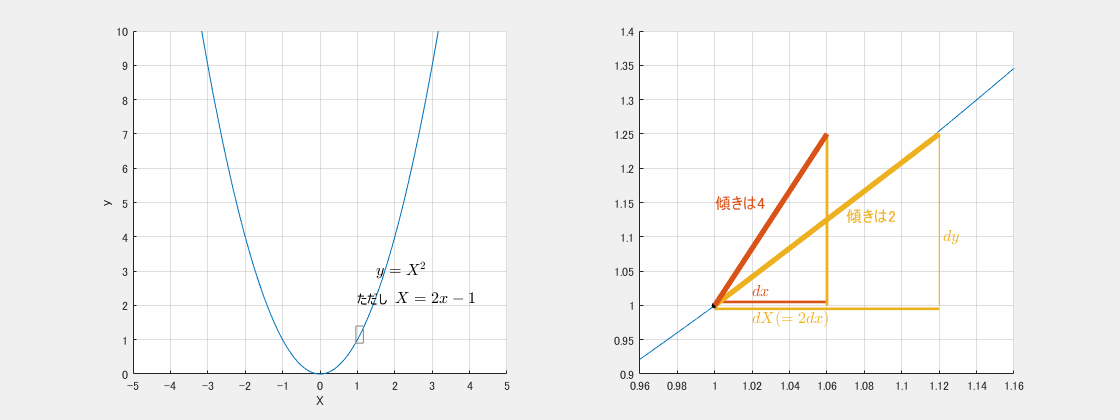
が知りたいわけです。下の動画でそのイメージを理解します。右図は左図の $X=1$ 付近にある四角部分であり、拡大図です。
横軸を $X$ にしたグラフで $\displaystyle\frac{dy}{dX}$ を求める：黄の傾き
上の動画の左の図は $X=2x-1$ と置くことにより元の式を $y=X^2$ としてグラフを描いたものです。まずこの $y=X^2$ に於いて $X$ で微分したもの $\displaystyle\frac{dy}{dX}$ は、$2X$ です。
$$\displaystyle\frac{dy}{dX} = 2X\tag{1}\label{p144eq1}$$
$dX$ と $dx$ の歩みの違いを考える：赤の歩みは遅い
しかし、本当に求めたいのは $\displaystyle\frac{dy}{dx}$ です。分母である $dX$ と $dx$ の歩み違いを考えます。いま、
$$X=2x-1$$
と置いたわけなので、$x$ が $dx$ 進んだ時(アニメーションの赤線)、$X$ はその2倍の $2dx$ 進みます(同黄線)。そうすると、求めたかったのは赤の傾きなので、黄の2倍になります。この2倍という数字がどこからきているのか今一度おさらいすると、
$$X=2x-1$$
の関係式からであり、$X$ は $x$ の2倍速く進む、つまり、
$$dX=2dx\tag{2}\label{p144eq2}$$
です。次にこれらを結び付けます。
両者を結び付けて $\displaystyle\frac{dy}{dx}$ が求まる
\eqref{p144eq2} を \eqref{p144eq1} に代入すると、
$$\displaystyle\frac{dy}{2dx}=2X$$
つまり、
\begin{eqnarray}
\frac{dy}{dx} &=& 2\cdot2X\\
&=& 2\cdot 2(2x-1)
\end{eqnarray}
となり、$\displaystyle\frac{dy}{dx}$ が求められました。
式変形を振り返り理解を整理する
式変形を振り返ると \eqref{p144eq2} を \eqref{p144eq1} に代入したわけですが、それは次のように式変形していることにほかなりません。
- $\displaystyle\frac{dy}{dX}=\displaystyle\frac{dy}{dx}\cdot\displaystyle\frac{dx}{dX}$
なぜなら、上の動画で見た通り、$\displaystyle\frac{dy}{dX}$ の値（黄の傾き）は、$\displaystyle\frac{dy}{dx}$ の値（赤の傾き）に比べて $\displaystyle\frac{dx}{dX}\left(=\displaystyle\frac{1}{2}\right)$ 倍だからです。
そして最終的な理解としてはこれの左辺と右辺を逆にして、
$$\frac{dy}{dx}=\frac{dy}{dX}\cdot\frac{dX}{dx}$$
としましょう。普通の分数のように計算して等しくなる感じです。
これこそが合成関数の微分です。微分の連鎖律とも言います。英語では chain rule と言い、まさに分数の鎖がつながっている様子です。
ひとつ前の例題で $x$ の係数が $1$ の時にはこのことを意識しなかったですが、なぜでしょうか。それは、$X=x-1$ と置換した際には、$x$ の変化量 $dx$ と $X$ の変化量 $dX$ は同じ、つまり $\displaystyle\frac{dX}{dx}=1$ だったためにそれほど意識しなくてもよかったというわけです。
微分の連鎖律を使いこなす
例1：$y=(2x-1)^2$ の微分 かっこのままで微分する
先ほどと同じ例題ですが、復習を兼ねて整理します。先ほどは $X=2x-1$ と置いて式を書き換えましたが、置換した気持ちをそのままに次のようにとらえましょう。
\begin{eqnarray}
\displaystyle\frac{dy}{dx} &=& \displaystyle\frac{d(2x-1)^2}{d(2x-1)}\cdot\displaystyle\frac{d(2x-1)}{dx}\\
&=& 2(2x-1)^1\cdot 2
\end{eqnarray}
もちろん、慣れなければ素直に置換して式変形をしていけばよいです。
例2：$y=\sin^2 x$ の微分
$X=\sin x$ と置換すれば $y=X^2$ となるので、
- $\displaystyle\frac{dy}{dX} = 2X$
- $\displaystyle\frac{dX}{dx} = \cos x$
から、
\begin{eqnarray}
\displaystyle\frac{dy}{dx} &=& \displaystyle\frac{dy}{dX}\cdot\displaystyle\frac{dX}{dx}\\
&=& 2X\cdot\cos x\\
&=& 2\sin x\cdot\cos x
\end{eqnarray}
です。
これも、例1のように「かっこのまま」っぽく、次のようにとらえてもよいです。
\begin{eqnarray}
\displaystyle\frac{dy}{dx} &=& \displaystyle\frac{d\sin^2 x}{d\,\sin x}\cdot\displaystyle\frac{d\,\sin x}{dx}\\
&=& 2\sin x\cdot\cos x
\end{eqnarray}
まとめ
合成関数の微分を理解しました。微分が鎖のようにつながるイメージから「連鎖律」と言います。普通の分数のように計算して等しくなる感じで、次のようなイメージです。
$$\frac{dy}{dx}=\frac{dy}{\cancel{dX}}\cdot\frac{\cancel{dX}}{dx}$$
この気持ちを持ってかっこのままでの微分を行いました。次のようなイメージです。
\begin{eqnarray}
\displaystyle\frac{dy}{dx} &=& \displaystyle\frac{d(2x-1)^2}{d(2x-1)}\cdot\displaystyle\frac{d(2x-1)}{dx}\\
&=& 2(2x-1)^1\cdot 2
\end{eqnarray}
\begin{eqnarray}
\displaystyle\frac{dy}{dx} &=& \displaystyle\frac{d\sin^2 x}{d\,\sin x}\cdot\displaystyle\frac{d\,\sin x}{dx}\\
&=& 2\sin x\cdot\cos x
\end{eqnarray}
この記事により合成関数の微分の際にわざわざ文字で置き換えることなく、ストレスなく計算できるようになっていただければ幸いです。
なお、この考え方を逆にすることにより置換積分もかっこのままで行うことができます。↓の記事で取り上げています。
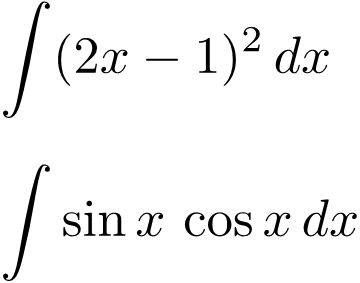
コメント