【直線に関して対称な点】楽に求める方法5選　基本から裏ワザ的方法まで

　内積の方法（射影ベクトル）が理解できれば楽に求められます。これが難しいと感じる場合でも、複数のアイデアを載せていますのでお気に入りを見つけてください。

初級：傾きの積を利用

　この解法は理屈は簡単ですが、その分計算量が多く面倒です。

多少楽に求めるテクニックはあり、「その2」の直線の式を求めるところではリンクに示すように「直線の式を一行で書く」ことができます。

その1：連立方程式を立てて解く方法

　この解法は、求めたい点 $\mathrm{Q}$ を $(a,b)$ と置いて連立方程式を立てますが、現時点では点 $\mathrm{Q}$ がどこにあるのかわからない状態なので、点 $\mathrm{Q}$ が彷徨さまようイメージです。こんなイメージ↓です。

　点 $\mathrm{Q}$ がどこか分からないので彷徨っています。しかし、点 $\mathrm{Q}$ に対応して点 $\mathrm{H}$ は定まっています。そして、青の線と赤の線が垂直で、かつ点 $\mathrm{H}$ が青の直線上の点にあるようなところを探しています。

解

　点 $\mathrm{Q}$ の座標を $(a,b)$ と置く。このとき、$\mathrm{PQ}$ の傾きは
$$\frac{b-4}{a-(-1)}$$
であり、それが傾き $-\displaystyle\frac{1}{2}$ になればよいから、
$$\frac{b-4}{a-(-1)}=-\frac{1}{2}\tag{1}\label{p1355eq1-1}$$

一方、このとき点 $\mathrm{H}$ の座標は
$$\left(\frac{-1+a}{2},\,\frac{4+b}{2}\right)$$
であり、この点が直線 $y=2x+1$ 上にあるから、
$$\frac{4+b}{2}=2\times\frac{-1+a}{2}\tag{2}+1\label{p1355eq1-2}$$

$\eqref{p1355eq1-1}$, $\eqref{p1355eq1-2}$ を解いて、
$$a=3,\; b=2$$

よって、

$$\mathrm{Q}(3,2)$$

その2：垂直な直線との交点を求めて解く方法

　この解法は、点 $\mathrm{P}$ を通り直線 $y=2x+1$ に垂直な直線との交点 $\mathrm{H}$ を求め、同じだけ向こう側が求める点 $\mathrm{Q}$ である、とする解法です。こんなイメージ↑です。

　点 $\mathrm{P}$ を通り傾きが $-\displaystyle\frac{1}{2}$ の赤の線が表れることで、その線と青の線との交点 $\mathrm{H}$ が求まります。

その後、 $\mathrm{P}$ から $\mathrm{H}$ までの道のりを数え、同じだけ $\mathrm{H}$ から進んだところが求めるべき点 $\mathrm{Q}$ です。

解

　点 $\mathrm{P}$ を通り傾き $-\displaystyle\frac{1}{2}$ の直線の方程式は、
$$y=-\frac{1}{2}(x+1)+4\tag{1}\label{p1355eq2-1}$$
この直線と元の直線
$$y=2x+1\tag{2}\label{p1355eq2-2}$$
との交点を $\mathrm{H}$ とすると、 $\mathrm{H}$ の座標は $\eqref{p1355eq2-1}$, $\eqref{p1355eq2-2}$ を解いて、
$$x=1,\; y=3$$
つまり、$\mathrm{H}(1,3)$。

求めるべき点 $\mathrm{Q}$ は、$\mathrm{P}$ から $\mathrm{H}$ まで進んだ分、 $\mathrm{H}$ から同じだけ進んだ点である。
よって、

$$\mathrm{Q}(3,2)$$

解説：直線の式は一行で書ける

　上記の解では、

点 $\mathrm{P}$ を通り傾き $-\displaystyle\frac{1}{2}$ の直線の方程式は、
$$y=-\frac{1}{2}(x+1)+4$$

と何気なく書いていますが、何気なく書けるようになれると楽です。↓の記事でそれが書けるようになります。

中級：法線ベクトルを利用

　計算量はぐっと減ります。法線ベクトルという概念さえわかれば理屈も分かりやすいです。法線ベクトルの概念はこちらのページ↓の「法線ベクトルを利用」をご覧ください。

その3：ベクトル方程式で解く方法

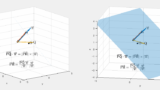
　この解法ではベクトル方程式という耳慣れない言葉が出てきてしまいましたが、難しくはないです。ベクトル方程式はベクトルの長さを調整する変数（媒介変数という）を用いてベクトルの行き先を規定します。こんなイメージです。

より詳しくはこの記事↓を見てください。3次元空間での説明ですが、2次元でも同じです。

　さて、$2x-y=-1$ の法線ベクトルは $\begin{pmatrix}2 \\ -1 \end{pmatrix}$ であり、点 $\mathrm{P}$ からこの方向に赤の矢印が伸びていきます。そして、青の矢印にぶつかったところから、さらに同じだけ進んだところが点 $\mathrm{Q}$ です。

解

　直線 $2x-y=-1$ の法線ベクトルは $\begin{pmatrix}2 \\ -1 \end{pmatrix}$ なので、
点 $\mathrm{P}$ を通りこの法線ベクトルを持つ直線は媒介変数 $t$ を用いて
$$\begin{pmatrix}x \\ y \end{pmatrix} = \begin{pmatrix}-1 \\ 4 \end{pmatrix} + t \begin{pmatrix}2 \\ -1 \end{pmatrix}$$
と書ける。この直線が $2x-y=-1$ に交わる点を点 $\mathrm{H}$ とすると、これに代入して、
$$2(-1+2t)-(4-t)=-1$$
$$t=1$$
つまり、$\mathrm{H}(1,3)$。求める点 $\mathrm{Q}$ はさらに同じだけ進んだ点なので、$t=2$ を代入した点である。

よって、

$$\mathrm{Q}(3,2)$$

上級：内積(射影ベクトル)を利用

　理屈は難しいですが、一度分かれば病みつきになります。射影ベクトルの概念はこちらのページ↓の「内積(射影ベクトル)を利用」をご覧ください。

なおここでは求める対象点を $\mathrm{R}$ にし、点 $\mathrm{Q}$ を別の点として使用しています。

その4：射影ベクトルを求める方法1

　この解法では垂線の足 $\mathrm{H}$ が一発で求められます。その後は、 $\mathrm{PH}$ と同じ分だけ動けば点 $\mathrm{R}$ です。こんなイメージです。

　内積を用いて $\overrightarrow{\mathrm{QA}}$ 上に $\overrightarrow{\mathrm{QP}}$ を射影して点 $\mathrm{H}$ を求めます。点 $\mathrm{H}$ が求まれば、 $\mathrm{PH}$ と同じだけ動いて点 $\mathrm{R}$ を求めます。

　なお、$\overrightarrow{\mathrm{QA}}$ はより単純な $\begin{pmatrix}1 \\ 2 \end{pmatrix}$ でもかまいませんが、求めるべき $\overrightarrow{\mathrm{QH}}$ との混同を避けるため、あえて $\begin{pmatrix}2 \\ 4 \end{pmatrix}$ にしました。

　また、$\mathrm{Q}$ の取り方は、今考えている直線 $y=2x+1$ 上ならどこでもよいです。別の点でもご自身で確かめてみてください。

解

　点 $(0,1)$を $\mathrm{Q}$、直線 $y=2x+1$ 上の点 $(2,5)$ を $\mathrm{A}$ とすると、
$\overrightarrow{\mathrm{QA}}=\begin{pmatrix}2 \\ 4 \end{pmatrix}$, $\overrightarrow{\mathrm{QP}}=\begin{pmatrix}-1 \\ 3 \end{pmatrix}$ であるから $\overrightarrow{\mathrm{QH}}$ は、

$$\begin{eqnarray} \overrightarrow{\mathrm{QH}} &=& \frac{\overrightarrow{\mathrm{QA}}\cdot\overrightarrow{\mathrm{QP}}}{|\overrightarrow{\mathrm{QA}}|^2}\cdot\overrightarrow{\mathrm{QA}}\\ &=& \frac{\begin{pmatrix}2 \\ 4 \end{pmatrix}\cdot\begin{pmatrix}-1 \\ 3 \end{pmatrix}}{\left|\begin{pmatrix}2 \\ 4 \end{pmatrix}\right|^2}\cdot\begin{pmatrix}2 \\ 4 \end{pmatrix}\\ &=& \frac{10}{20}\begin{pmatrix}2 \\ 4 \end{pmatrix}\\ &=& \begin{pmatrix}1 \\ 2 \end{pmatrix} \end{eqnarray}$$

つまり、$\mathrm{H}(1,3)$。求める点 $\mathrm{R}$ はさらに $\overrightarrow{\mathrm{PH}} = \begin{pmatrix}2 \\ -1 \end{pmatrix}$ だけ動いたもの。
よって、

$$\mathrm{R}(3,2)$$

その5：射影ベクトルを求める方法2

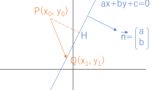
　先ほどとほとんど同じですが、射影するベクトルの選び方を変えて考えることができます。法線ベクトルを持ち出すところが少し戸惑う点かもしれないですが、こちらの方が「点と直線の距離」「点と平面の距離」を求める際にも便利ですのでおススメです。

解

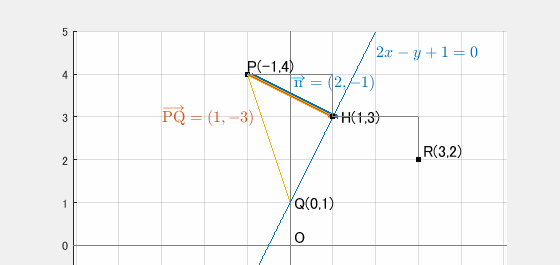
　直線 $y=2x+1$ 上の点の一つ $(0,1)$ を $\mathrm{Q}$ と置く。

直線 $y=2x+1$ は $2x-y+1=0$ なので、法線ベクトルの一つを $\overrightarrow{n}$ と置くと、$\overrightarrow{n}=\begin{pmatrix}2\\-1\end{pmatrix}$。

ここで、$\overrightarrow{\mathrm{PQ}}=\begin{pmatrix}1 \\ -3 \end{pmatrix}$ であり、点 $\mathrm{P}$ から直線 $y=2x+1$ に下した垂線の足を $\mathrm{H}$ と置くと、

$$\begin{eqnarray} \overrightarrow{\mathrm{PH}} &=& \frac{\overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{n}}{|\overrightarrow{n}|^2}\cdot\overrightarrow{n}\\ &=& \frac{\begin{pmatrix}1 \\ -3 \end{pmatrix}\cdot\begin{pmatrix}2 \\ -1 \end{pmatrix}}{\left|\begin{pmatrix}2 \\ -1 \end{pmatrix}\right|^2}\cdot\begin{pmatrix}2 \\ -1 \end{pmatrix}\\ &=& \frac{5}{5}\begin{pmatrix}2 \\ -1 \end{pmatrix}\\ &=& \begin{pmatrix}2 \\ -1 \end{pmatrix} \end{eqnarray}$$

つまり、$\mathrm{H}(1,3)$。求める点 $\mathrm{R}$ はさらに $\overrightarrow{\mathrm{PH}} = \begin{pmatrix}2 \\ -1 \end{pmatrix}$ だけ動いたもの。
よって、

$$\mathrm{R}(3,2)$$

まとめ

　直線に関して対称な点を複数の解法で解きました。これら複数の解法を持っておくことで余裕をもって問題に接することができます。

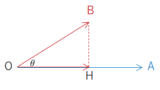
また、上記の「射影ベクトルを求める方法2」の考え方を使えば、点と直線の距離では下記記事↓のようにスマートに求めることができます。